MATH 2121: Lecture 3

Date: 2024-09-10 13:40:28

Reviewed:

Topic / Chapter: Vectors, Linear Combination, and Span

summary

❓Questions

Notes

Vectors

Vector terminology
- vector: matrix with exactly one column
  - 👨‍🏫 until we discuss vector spaces
  - $[1], 1235, [76],$ etc.
  - aka: column vectors
- general vector $v = v_{1} v_{2} ⋮ v_{n}$
  - where $v_{1} \in R$
- two vectors $u, v$ : equal if same no. of rows & same entries for each row
- size of vector: no. of rows
- vectors of same size: can be added $v_{1} v_{2} ⋮ v_{n} + u_{1} u_{2} ⋮ u_{n} = u_{1} + v_{1} u_{2} + v_{2} ⋮ u_{n} + v_{n}$
  - and $u + v = v + u$
- if $c \in R$ is a scala, then: scala multiple, $c v$ is: $c v = c v_{1} v_{2} ⋮ v_{n} = c v_{1} c v_{2} ⋮ c v_{n}$
- subtraction is defined as $u - v = u + (- 1 \cdot v)$
- $R^{n}$ : set of all vectors w/ exactly $n$ rows
- vectors $a = [a_{1} a_{2}] \in R^{2}$ : identified as arrows in the Cartesian plane
  - $(0, 0) \to (a_{1}, a_{2})$
- ⭐ proposition: sum of two vectors, $a + b = b + a$ can be represented as arrow towards opposite vector of the parallelogram w/ sides $a, b$
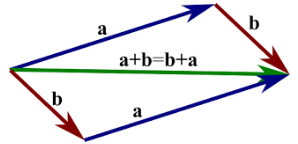
  - proof:
    - let $\frac{a _{2}}{a _{1}}, \frac{b _{2}}{b _{1}}$ be slopes of arrow $a, b$
    - then slope of arrow from end of $b$ to $a + b$ (line 1): $\frac{( a _{2} + b _{2} ) - b _{2}}{( a _{1} + b _{1} ) - b _{1}} = \frac{a _{2}}{a _{1}}$
    - slope of arrow from end of $a$ to $a + b$ (line 2): $\frac{( a _{2} + b _{2} ) - b _{2}}{( a _{1} + b _{1} ) - b _{1}} = \frac{b _{2}}{b _{1}}$
    - thus, the diagram made by these 4 vectors is a parallelogram
    - the opposite vertex: where line 1,2 meets: $a + b$
    - thus the endpoint = opposite vertex of parallelogram from origin
- zero vector in $R^{n}$ : vector with all entries being 0
  - symbol 0 is used for both number 0 and zero vector in $R^{n}$ for any $n$

Linear Combination

Linear combinations
- suppose $v_{1}, v_{2}, \dots, v_{p} \in R^{n}$ are vectors
- and $c_{1}, c_{2}, \dots, c_{p} \in R^{n}$ are scalars
- then linear combination: $y = \sum_{i = 1}^{p} c_{i} v_{i}$
- in language: " $y$ is combination of $v_{1}, v_{2}, \dots, v_{p} \in$ with coefficients $c_{1}, c_{2}, \dots, c_{p} \in$ "
- ⭐ proposition: a vector equation of the form
  - $\sum_{i = 1}^{n} x_{i} a_{1} = b$
    - where $x_{i}$ are variables and $a_{i}, b \in R^{m}$ are vectors
  - has the same solution w/ the linear system w. augmented matrix $A = [a_{1} a_{2} \dots a_{n} b]$
  - i.e. $b$ being lin. combination of $a_{i}$ $⟺$ lin. sys. being consistent (1 answer)

Span

Span
- span of a finite set of vectors $v_{i} \in R^{n}$ : set of all vectors $y \in R^{n}$
  - that are linear combinations of $v_{i}$
  - and is denoted by: $R -span {v_{1}, v_{2}, \dots, v_{p}}$
    - or $span {v_{1}, v_{2}, \dots, v_{p}}$
- or, more directly: $R -span {v_{1}, v_{2}, \dots, v_{p}} = {i = 1 \sum p a_{i} v_{i} : a_{1}, a_{2}, \dots, a_{p} \in R}$
- example
  - $R -span {0} = {a 0 : a \in R} = {0}$
    - unless: span is an infinite set
  - span of non-zero $v$ : $R -span {v} = {a v : a \in R}$
    - all scalar multiples of $v$
    - i.e. line
  - for non-zero $v, w$ ; $R -span {v, w} = {a v + b w : a, b \in R}$
  - if $v = c w$ ; $R -span {v, w} = R -span {w}$
    - i.e. line
  - otherwise: no simpler way of describing $R -span {v, w}$
    - 👨‍🏫 unless you want to say: "the set of all vectors of the form $a v + b w$ where $a$ and $b$ are arbitrary real numbers."
Visualizing span
- span of 0: single point consisting of origin
- span: collection of vectors belonging to the same line through the origin
- for $R^{2}$ , span of $v_{1}, v_{2}, \dots, v_{p}$ : a plane not a line
  - all combinations of two non-parallel vectors
  - i.e. we can get any vector in Cartesian by combining 2 non-parallel vectors
Remarks
- often, separate word exists for operation, verb doing the operation, and the result of operation
  - e.g. addition-add-sum
- $R -span$ : also an operation
  - input: collection of vectors w/ same size
  - output: set of vectors w/ same size as the input
- for span, names are:
  - operation: span
  - output $S$ of span operation on $v_{i}$ : the span of $v_{i}$
  - or: (as a verb) $v_{i}$ spans the set $S$
  - $w \in R^{n}$ is spanned by $v_{1}$ : means $w \in S$
- 👨‍🏫 span of an infinite collection of vectors in $R^{n}$ : not covered yet
  - think of it as set of all vectors in $R^{n}$
  - s.t. are linear combinations of a finite subset of collection of input vectors
  - finiteness: required as linear combinations aca only be formed w/ finite list of vectors
    - no general way to compute infinite sums of vectors
  - now: $R -span$ : takes any set of vectors in $R^{n}$ , and produces a set of vectors in $R^{n}$
    - as input type == output type
    - $R -span$ can be composed with itself
  - above operation: idempotent in that
    - $S \subset R^{n}$ is any set, then $R -span (R -span (S)) = R -span (S)$

MATH 2121: Linear Algebra