This will be a first course in linear algebra, from an applied perspective. The main topics covered will include solving linear systems of equations, vector spaces, matrices, linear mappings and matrix forms, inner products, orthogonality, eigenvalues and eigenvectors, and symmetric matrices. No prior knowledge of matrix algebra is assumed.

If you submit correct solutions to extra practice problems, then you can earn extra credit. You can earn up to 5% extra credit for your course grade in this way over the whole semester. See the instructions for the offline homework assignments on the course website.

• Introduction

  • for contact: Discord is also an option
  • online HW: 5%; due every Monday
    • WebWork w/ some attempt
    • computing value
  • offline PSETs; due every Wednesday
    • choose 4 problem; exam-like course
    • no extra harsh grading
    • 5% bonus for up to 4 bonus problems
  • assignment submission: talk to TA
  • A-range: w/ cutoff that's based on exam difficulty
    • ~= absolute grading in 1013/4

• Notation:

  • $\mathbb{R}$ denotes the real numbers.
  • $\mathbb{Q}$ denotes the rational numbers p/q.
  • $\mathbb{Z}$ denotes the integers $\{\dots ,-1,0,1,\dots \}$
  • $\mathbb{N}$ denotes the nonnegative integers $\{0,1,2,\dots \}$.
  • Ellipsis ($\dots$) notation: we write $a_1,a_2,\dots ,a_7$ instead of the full list .

• Linear equation

  • let $n\in {\mathbb{Z}}^{+}$; $x_1,x_2,\dots ,x_n$ be var. and $a_1,a_2,\dots a_n,b$ constants $\in \mathbb{R}$
    • 👨‍🏫 prefers $x_1,x_2,x_3$ than $x,y,z$
  • linear equation in var $x_1,x_2,\dots x_2$ can be written in:
    • ${\sum }_{i=1}^n{a}_i{x}_i=b$
    • examples
      • $4x_1+5x_2-\pi x_3=-1$
      • $0=0$
      • $0=1$ // equation, but a false statement
        • corresponds to case $a_1=0,a_2=0,a_2=0,b=1$
    • 👨‍🎓as long as there is no exponent $\notin \{0,1\}$
      • and no var. is multiplied with another var.
      • or: var is not in exponent
      • $\sqrt{x^2}=>|x|$; not considered as linear
  • linear system: a list of linear equations
  • solution to linear system: assignment of val to var s.t. all equations in the system are simultaneously true
    • solution: non-zero if at least one assignment of var. $\ne 0$
    • e.g. $\{\begin{array}{l}{x}_1+x_2=7\\ x_2-x_1=1\end{array}$
      • has solution $(x_1,x_2)=(3,4)$
      • linear systems: equivalent if their solution are the same (or: have the same set of solutions)
        • and with the same variable sets
  • any linear system: w/ 0, 1, or infinitely many solutions
    • if a system has 2 or more solutions -> has $\infty$ solutions
    • lin. sys w/ no solution: inconsistent
    • lin. sys w/ exactly 1 solution: consistent

• Proof on No. of Solutions on Lin Alg Systems of Equation

  • theorem: A linear system in two variables $x_1$ and $x_2$ has either 0, 1, or infinitely many solutions
  • by geometry
    • a solution to one lin. equation: represents a point io a line
    • solution to a system of 2-var lin. eq.: represents intersection of all lines defined by the equations
    • however: collections of lines must either:
      • intersect at one point
      • intersect at no point
      • infinitely many solutions
        • i.e. all equations: represent the same line
    • 👨‍🎓 what if we are on spherical, or non-euclidean plane?
  • by algebra
    • just check if lin. sys. has 2 different solution
    • given lin. sys., define the associated homogeneous system
      • where you set $b=0$
    • if $(s_1,s_2)$ is solution to the starting system
      • and $(t_1,t_2)$ solution to associated homogeneous system.
      • then $(s_1+t_1,s_2+t_2)$ is also the solution to starting system
      • as $\sum a_i(s_i+t_i)=\sum a_i{s}_i+\sum a_i{t}_i=b+0=b$
    • if homogenous system has a non-zero solution, then it has infinite many solutions
      • can be obtained by multiplying $t_i$ to any real number, and adding to original solution
    • if starting sys. has two different solutions: $(s_1,s_2)$ and $(r_1,r_2)$
      • then $(t_1,t_2,)=(s_1-r_1,s_2-r_2)$ is a non-zero solution to homogenous system
    • as $\sum a_i(s_i-r_i)=\sum a_i{s}_i-\sum a_i{r}_i=b-b=0$

• Matrix

  • matrix: rectangular array of numbers
    • e.g. $\left[\begin{array}{c}\sqrt{2}\end{array}\right]$, $\left[\begin{array}{cc}1.1& -1.1\\ 1.1& 1.2\end{array}\right]$, $\left[\begin{array}{ccc}1& 7& -1\\ 0& 4& 3\end{array}\right]$
  • general matrix: denoted by $A=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\end{array}\right]$
    • where $A_{23}$ is read as "A, two, three"
  • matrix $A$ w/ $m$ rows & $n$ columns: called "$m\times n$" or "$m$-by-$n$"
    • index: starts from 0; top->down and left->right
    • entry in row $i$, col $j$ of matrix $A$: $A_{ij}$
      • or "entry of A in position $(i,j)$"
    • 👨‍🏫 position itself: also called "position $(i,j)$"
  • zero matrix: matrix filled w/ 0

• Augmented Matrix of the System

  • essential information of sys. of equation: set of $a$s and $b$ in a matrix

    $$\begin{array}{rl}{x}_1-2x_2+x_3& =0\\ 2x_2+8x_3& =8\\ 5x_1-5x_3& =10\end{array}$$

  • changes into $\left[\begin{array}{cccc}1& -2& 1& 0\\ 0& 2& -8& 8\\ 5& 0& -5& 10\end{array}\right]$ OR $\left[\begin{array}{cccc}1& -2& 1& 0\\ 0& 2& -8& 8\\ 5& 0& -5& 10\end{array}\right]$

  • bar: can be anywhere, but often used to separate constant terms

  • coefficient matrix of system: w/o constant terms

    $\left[\begin{array}{ccc}1& -2& 1\\ 0& 2& -8\\ 5& 0& -5\end{array}\right]$

• Solving linear systems

  • solve by transforming augmented matrix for certain operations

    1. add $-5\times$ equation 1 to equation 3

       $\left[\begin{array}{cccc}1& -2& 1& 0\\ 0& 2& -8& 8\\ 0& 10& -10& 10\end{array}\right]$

    2. multiply equation 2 by $1/2$

       $\left[\begin{array}{cccc}1& -2& 1& 0\\ 0& 1& -4& 4\\ 0& 10& -10& 10\end{array}\right]$

    3. add $-10\times$ equation 2 to equation 3

       $\left[\begin{array}{cccc}1& -2& 1& 0\\ 0& 1& -4& 4\\ 0& 0& 30& -30\end{array}\right]$

    4. multiple equation 3 by $1/30$

       $\left[\begin{array}{cccc}1& -2& 1& 0\\ 0& 1& -4& 4\\ 0& 0& 1& -1\end{array}\right]$

  • augmented matrix of the system is triangular if all entries in position $(i,j)$ w/ $i>j$ are zero
  • triangular system: can be solved easily from bottom-up
    • last equation: $x_3=-1$
    • which substitutes second eq. into $x_2-4x_4=4\Rightarrow x_2-4(-1)=4\Rightarrow x_2=0$
    • then, the first: $x_1-2x_2+x_3=x_1=2(0)+(-1)=0\Rightarrow x_1=1$

• Row operations

  • we have used following elementary row operations on the augmented matrix of the system

  1. Replacement: replace one row by the sum of itself & a multiple of another row

     $\left[\begin{array}{cc}1& 2\\ 5& 6\end{array}\right]\to \left[\begin{array}{cc}1& 2\\ 6& 8\end{array}\right]$ or $\left[\begin{array}{cc}1& 2\\ 5& 6\end{array}\right]\to \left[\begin{array}{cc}501& 602\\ 4& 6\end{array}\right]$

  2. Scaling: multiply all entries in a row w/ non-zero number

     $\left[\begin{array}{cc}1& 2\\ 5& 6\end{array}\right]\to \left[\begin{array}{cc}1& 2\\ -500& -600\end{array}\right]$

  3. Interchange: swap two rows

     $\left[\begin{array}{cc}1& 2\\ 5& 6\end{array}\right]\to \left[\begin{array}{cc}5& 6\\ 1& 2\end{array}\right]$

• Row equivalence

  • two matrices: row equivalent if one can be transformed to the other
    • through a seq. of row operations
  • each row operations are revertible
    • 👨‍🏫 can you show why?
    • replacement: as another row, used for addition, remains uncontaminated, you can subtract it back (with coefficient)
    • scaling: as one cal multiply reciprocal
    • interchange: as one can swap back

• Introduction

  • goal: give an algorthm to determine how many solutions (0, 1, $\infty$) does a lin. sys. have
    • and find out the value of solutions, when they exist
  • such algorithm: row reduction to echelon form
    • formalize the way we solve lin. sys.also called: Gausiian elimination

• Defining reduced echelon form

  • row in matrix: nonzero if "not every entry in the row" is zero
    • $\exists A_{ij}\in A_{ij},A_{ij}\ne 0$
    • nonzero column: defined similarly
  • leading entry in a row: first non-zero entry in the row
    • starting from left to right
  • matrix of size $m\times n$ is in echelon form if:
    1. if a row is nonzero: every row above it is also nonzero
    2. the leading entry in a nonzero row: strictly right of the leading entry of any earlier row
       • 👨‍🎓 i.e. in somewhat triangular form?
    3. if a row is nonzero: every entry below its leading entry in the same column is zero
       • implied from the second principle
  • by definition
    • every one-row matrix is in echelon form
    • one-column matrix in echelon form: where * is any number $$\left[\begin{array}{c}\ast \\ 0\\ 0\\ ⋮\\ 0\end{array}\right]$$
  Examples

  • echelon form: $$\left[\begin{array}{cccccccccc}0& 0& 5& \ast & \ast & \ast & \ast & \ast & \ast & \ast \\ 0& 0& 0& 6& \ast & \ast & \ast & \ast & \ast & \ast \\ 0& 0& 0& 0& 0& 0& 7& \ast & \ast & \ast \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 9\end{array}\right]$$
  • NOT echelon form: $$\left[\begin{array}{cccccccccc}0& 0& 5& \ast & \ast & \ast & \ast & \ast & \ast & \ast \\ 0& 0& 6& \ast & \ast & \ast & \ast & \ast & \ast & \ast \\ 0& 0& 0& 0& 0& 0& 7& \ast & \ast & \ast \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 9\end{array}\right]$$
  • a matrix in echelon form is reduced is
    1. each nonzero row has leading entry 1
    2. the leading 1 in each nonzero row is the only nonzero number in its column
  • reduced echelon form: matrix in echelon form that is reduced
    • 👨‍🎓 $\approx$ solved?
  • reduced echelon form looks like: $$\left[\begin{array}{cccccccccc}0& 0& 1& 0& \ast & \ast & 0& \ast & \ast & 0\\ 0& 0& 0& 1& \ast & \ast & 0& \ast & \ast & 0\\ 0& 0& 0& 0& 0& 0& 1& \ast & \ast & 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]$$
  • ⭐ theorem: each matrix $A$ is row equivalent to exactly one matrix $RREF(A)$ in reduced echelon form
  • $RREF(A)$: reduced echelon form of $A$

• Solving a linear system from reduce echelon form

  • pivot position in a matrix $A$: location containing a leading 1 in $RREF(A)$

    • aka: $pivot$

  • pivot column in a matrix A: column containing a pivot position

  • for lin. sys. in $x_1,x_2,\dots ,x_n$ with aug. matrix $A$

    • the var $x_i$ is ...
      • basic if $i$ is a pivot column of $A$
      • free if $i$ is not a pivot column of $A$

  • case study

    $$RREF(A)=\left[\begin{array}{cccc}1& 0& -5& 1\\ 0& 1& 1& 4\\ 0& 0& 0& 0\end{array}\right]$$

    • which means system:

      $$\{\begin{array}{l}{x}_1-5x_3=1\\ x_2+x_3=4\\ 0=0\end{array}$$

      • $x_1,x_2$ are basic
      • and $x_3$ is free

    • to solve the system: choose any values for the free var., and solve for the basic var.

    • solution to above system: all in form

      • $(x_1,s_2,s_3)=(5a+1,4-a,a|a\in \mathbb{R})$

  • theorem: consider a lin. sys. whose augmented matrix is A

    • the system has 0 solutions / is inconsistent
      • if the last column of $A$ contains a pivot
      • which the row will look like: $\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 1\end{array}\right]$
        • i.e. equivalent of saying $0=1$
    • the system has only 1 solution
      • if there are no free variables and the last column is not a pivot
    • otherwise: the system has infinitely many solutions

  • once $RREF(A)$ is computed and free / basic var. are identified

    • we can write down all solutions to system as in the above example
    • let all free var. to be arbitrary, and solve it for basic var.

• Computing reduced echelon form

  • algorithm to compute $RREF(A)$ has two parts
    • row reduction to echelon form
    • reducing it to $RREF(A)$
  • example
    • for general algorithm: input: $m\times n$ matrix $A$ $$A=\left[\begin{array}{cccc}0& 3& -6& 6\\ 3& -7& 8& -5\\ 3& -9& 12& -9\end{array}\right]$$
    • procedure

      1. begin with the leftmost nonzero column

         • this will be the pivot column, pivot being the top position
         • boxed: pivot position $$\left[\begin{array}{cccc}\boxed{0}& 3& -6& 6\\ 3& -7& 8& -5\\ 3& -9& 12& -9\end{array}\right]$$

      2. select a nonzero entry in the current pivot column

         • if needed: perform row operation to swap the row with the top one $$\left[\begin{array}{cccc}\boxed{0}& 3& -6& 6\\ 3& -7& 8& -5\\ 3& -9& 12& -9\end{array}\right]\to \left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& 3& -6& 6\\ 3& -9& 12& -9\end{array}\right]$$

      3. use row operations to create zeros below the boxed pivot position $$\left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& 3& -6& 6\\ 3& -9& 12& -9\end{array}\right]\to \left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& 3& -6& 6\\ 0& -2& 4& -4\end{array}\right]$$

      4. repeat steps 1-3 on the bottom right sub-matrix

         $$\left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& \boxed{3}& -6& 6\\ 0& -2& 4& -4\end{array}\right]\to \left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& \boxed{3}& -6& 6\\ 0& 0& 0& 0\end{array}\right]$$

      5. now: we have a echelon form: now reduce it (w/ replacements) $$\left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& \boxed{3}& -6& 6\\ 0& 0& 0& 0\end{array}\right]$$

      • now: rescale rightmost pivot, and cancel entries above rightmost pivot
        • repeat (heading left) $$\begin{gathered} \to \left[\begin{array}{cccc}\boxed{3}& -7& 8& -5\\ 0& \boxed{1}& -2& 2\\ 0& 0& 0& 0\end{array}\right]\to \left[\begin{array}{cccc}\boxed{3}& 0& -6& 9\\ 0& \boxed{1}& -2& 2\\ 0& 0& 0& 0\end{array}\right] \\ \to \left[\begin{array}{cccc}\boxed{1}& 0& -2& 3\\ 0& \boxed{1}& -2& 2\\ 0& 0& 0& 0\end{array}\right] \end{gathered}$$
      • final result $$\left[\begin{array}{cccc}\boxed{1}& 0& -2& 3\\ 0& \boxed{1}& -2& 2\\ 0& 0& 0& 0\end{array}\right]$$
  • for a general matrix $A$: follow the algorithm below
    • input: $m\times n$ matrix $A$
    • procedure:
      1. begin with the leftmost nonzero column
         • i.e. the pivot column, position being the top position of column
      2. select a nonzero entry in current pivot column
         • swap rows as needed
      3. use row operations to create zeros in the entries below the pivot
      4. apply previous step for $(m-1)\times n$ sub-matrix that remains
         • repeat until the entire matrix is in echelon form
      5. start from the rightmost pivot position in matrix
         • rescale this row to have leading entry 1
         • use row operation to create zeros in entries in the same column as the pivot
         • repeat this for the pivot {above = left}
    • output: $RREF(A)$

• Problem 1

  1. write down augmented matrix of th linear system $$\begin{array}{r}\{\begin{array}{ll}2x_1+x_3+21x_4& =5\\ x_1+9x_2+8x_3+3x_4& =6\\ 3x_1-12x_4& =0\end{array}\end{array}$$
     • as of following: $$\left[\begin{array}{ccccc}2& 0& 1& 21& 5\\ 1& 9& 8& 3& 6\\ 3& 0& 0& 12& 0\end{array}\right]$$
  2. compute the reduced echelon form of the matrix
  • to echelon form $$\begin{array}{rl}\left[\begin{array}{ccccc}2& 0& 1& 21& 5\\ 1& 9& 8& 3& 6\\ 3& 0& 0& 12& 0\end{array}\right]& =\left[\begin{array}{ccccc}3& 0& 0& 12& 0\\ 2& 0& 1& 21& 5\\ 1& 9& 8& 3& 6\end{array}\right]\\ & =\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 2& 0& 1& 21& 5\\ 1& 9& 8& 3& 6\end{array}\right]\\ & =\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 2& 0& 1& 21& 5\\ 0& 9& 8& -1& 6\end{array}\right]\\ & =\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 0& 0& 1& 13& 5\\ 0& 9& 8& -1& 6\end{array}\right]\\ & =\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 0& 9& 8& -1& 6\\ 0& 0& 1& 13& 5\end{array}\right]\end{array}$$
  • to RREF $$\begin{array}{rl}\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 0& 9& 8& -1& 6\\ 0& 0& 1& 13& 5\end{array}\right]& =\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 0& 9& 0& -105& -34\\ 0& 0& 1& 13& 5\end{array}\right]\\ & =\left[\begin{array}{ccccc}1& 0& 0& 4& 0\\ 0& 1& 0& -35/3& -34/9\\ 0& 0& 1& 13& 5\end{array}\right]\end{array}$$
  3. how many solutions exists?
     • infinite, as there is a free variable, and the last column does not have a pivot

• Problem 2

  • find all solutions to following system $$\begin{array}{r}\{\begin{array}{ll}{x}_1-x_2-6x_3& =10\\ 2x_2+7x_3& =-10\\ x_1+x_2+x_3& =0\end{array}\end{array}$$
  • to matrix $$\begin{array}{rl}\left[\begin{array}{cccc}1& -1& -6& 10\\ 0& 2& 7& -10\\ 1& 1& 1& 0\end{array}\right]& =\left[\begin{array}{cccc}1& -1& -6& 10\\ 0& 2& 7& -10\\ 0& 2& 7& -10\end{array}\right]\\ & =\left[\begin{array}{cccc}1& -1& -6& 10\\ 0& 2& 7& -10\\ 0& 0& 0& 0\end{array}\right]\\ & =\left[\begin{array}{cccc}1& -1& -6& 10\\ 0& 1& 7/2& -5\\ 0& 0& 0& 0\end{array}\right]\\ & =\left[\begin{array}{cccc}1& 0& -5/2& 5\\ 0& 1& 7/2& -5\\ 0& 0& 0& 0\end{array}\right]\end{array}$$
  • infinitely many solution, as there is a free variable & last column is not a pivot

• Vector terminology

  • vector: matrix with exactly one column
    • 👨‍🏫 until we discuss vector spaces
    • $\left[\begin{array}{c}1\end{array}\right],\left[\begin{array}{c}1\\ 2\\ 3\\ 5\end{array}\right],\left[\begin{array}{c}\sqrt{7}\\ \sqrt{6}\end{array}\right],$ etc.
    • aka: column vectors
  • general vector $v=\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]$
    • where $v_1\in \mathbb{R}$
  • two vectors $u,v$: equal if same no. of rows & same entries for each row
  • size of vector: no. of rows
  • vectors of same size: can be added $$\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]+\left[\begin{array}{c}{u}_1\\ u_2\\ ⋮\\ u_n\end{array}\right]=\left[\begin{array}{c}{u}_1+v_1\\ u_2+v_2\\ ⋮\\ u_n+v_n\end{array}\right]$$
    • and $u+v=v+u$
  • if $c\in \mathbb{R}$ is a scala, then: scala multiple, $cv$ is: $$cv=c\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]=\left[\begin{array}{c}c{v}_1\\ c{v}_2\\ ⋮\\ c{v}_n\end{array}\right]$$
  • subtraction is defined as $u-v=u+(-1\cdot v)$
  • ${\mathbb{R}}^n$: set of all vectors w/ exactly $n$ rows
  • vectors $a=\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]\in {\mathbb{R}}^2$: identified as arrows in the Cartesian plane
    • $(0,0)\to (a_1,a_2)$
  • ⭐ proposition: sum of two vectors, $a+b=b+a$ can be represented as arrow towards opposite vector of the parallelogram w/ sides $a,b$
    • 
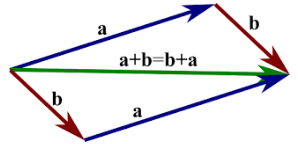
    • proof:
      • let $\frac{a_2}{a_1},\frac{b_2}{b_1}$ be slopes of arrow $a,b$
      • then slope of arrow from end of $b$ to $a+b$ (line 1): $\frac{(a_2+b_2)-b_2}{(a_1+b_1)-b_1}=\frac{a_2}{a_1}$
      • slope of arrow from end of $a$ to $a+b$ (line 2): $\frac{(a_2+b_2)-b_2}{(a_1+b_1)-b_1}=\frac{b_2}{b_1}$
      • thus, the diagram made by these 4 vectors is a parallelogram
      • the opposite vertex: where line 1,2 meets: $a+b$
      • thus the endpoint = opposite vertex of parallelogram from origin
  • zero vector in ${\mathbb{R}}^n$: vector with all entries being 0
    • symbol 0 is used for both number 0 and zero vector in ${\mathbb{R}}^n$ for any $n$

• Linear combinations

  • suppose $v_1,v_2,\dots ,v_p\in {\mathbb{R}}^n$ are vectors
  • and $c_1,c_2,\dots ,c_p\in {\mathbb{R}}^n$ are scalars
  • then linear combination: $y={\sum }_{i=1}^p{c}_i{v}_i$
  • in language: "$y$ is combination of $v_1,v_2,\dots ,v_p\in$ with coefficients $c_1,c_2,\dots ,c_p\in$"
  • ⭐ proposition: a vector equation of the form
    • ${\sum }_{i=1}^n{x}_i{a}_1=b$
      • where $x_i$ are variables and $a_i,b\in {\mathbb{R}}^m$ are vectors
    • has the same solution w/ the linear system w. augmented matrix $A=\left[\begin{array}{ccccc}{a}_1& a_2& \dots & a_n& b\end{array}\right]$
    • i.e. $b$ being lin. combination of $a_i$ $⟺$ lin. sys. being consistent (1 answer)

• Span

  • span of a finite set of vectors $v_i\in {\mathbb{R}}^n$: set of all vectors $y\in {\mathbb{R}}^n$
    • that are linear combinations of $v_i$
    • and is denoted by: $\mathbb{R}\text{-span}\{v_1,v_2,\dots ,v_p\}$
      • or $\text{span}\{v_1,v_2,\dots ,v_p\}$
  • or, more directly: $$\begin{gathered} \mathbb{R}\text{-span}\{v_1,v_2,\dots ,v_p\} \\ =\{\sum _{i=1}^p{a}_i{v}_i:a_1,a_2,\dots ,a_p\in \mathbb{R}\} \end{gathered}$$
  • example
    • $\mathbb{R}\text{-span}\{0\}=\{a0:a\in \mathbb{R}\}=\{0\}$
      • unless: span is an infinite set
    • span of non-zero $v$: $\mathbb{R}\text{-span}\{v\}=\{av:a\in \mathbb{R}\}$
      • all scalar multiples of $v$
      • i.e. line
    • for non-zero $v,w$; $\mathbb{R}\text{-span}\{v,w\}=\{av+bw:a,b\in \mathbb{R}\}$
    • if $v=cw$; $\mathbb{R}\text{-span}\{v,w\}=\mathbb{R}\text{-span}\{w\}$
      • i.e. line
    • otherwise: no simpler way of describing $\mathbb{R}\text{-span}\{v,w\}$
      • 👨‍🏫 unless you want to say: "the set of all vectors of the form $av+bw$ where $a$ and $b$ are arbitrary real numbers."

• Visualizing span

  • span of 0: single point consisting of origin
  • span: collection of vectors belonging to the same line through the origin
  • for ${\mathbb{R}}^2$, span of $v_1,v_2,\dots ,v_p$: a plane not a line
    • all combinations of two non-parallel vectors
    • i.e. we can get any vector in Cartesian by combining 2 non-parallel vectors

• Remarks

  • often, separate word exists for operation, verb doing the operation, and the result of operation
    • e.g. addition-add-sum
  • $\mathbb{R}\text{-span}$: also an operation
    • input: collection of vectors w/ same size
    • output: set of vectors w/ same size as the input
  • for span, names are:
    • operation: span
    • output $S$ of span operation on $v_i$: the span of $v_i$
    • or: (as a verb) $v_i$ spans the set $S$
    • $w\in {\mathbb{R}}^n$ is spanned by $v_1$: means $w\in S$
  • 👨‍🏫 span of an infinite collection of vectors in ${\mathbb{R}}^n$: not covered yet
    • think of it as set of all vectors in ${\mathbb{R}}^n$
    • s.t. are linear combinations of a finite subset of collection of input vectors
    • finiteness: required as linear combinations aca only be formed w/ finite list of vectors
      • no general way to compute infinite sums of vectors
    • now: $\mathbb{R}\text{-span}$: takes any set of vectors in ${\mathbb{R}}^n$, and produces a set of vectors in ${\mathbb{R}}^n$
      • as input type == output type
      • $\mathbb{R}\text{-span}$ can be composed with itself
    • above operation: idempotent in that
      • $S\subset {\mathbb{R}}^n$ is any set, then $\mathbb{R}\text{-span}(\mathbb{R}\text{-span}(S))=\mathbb{R}\text{-span}(S)$

• Matrix as vector operator

  • given $a_i\in {\mathbb{R}}^m,c\in {\mathbb{R}}^n$

    • $A=\left[\begin{array}{cccc}{a}_1& a_2& \dots & a_n\end{array}\right]$ and $v=\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]$

    • then matrix-vector product $Av\in {\mathbb{R}}^m$ $$\begin{array}{rl}Av& =\left[\begin{array}{cccc}{a}_1& a_2& \dots & a_n\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\\ ⋮\\ v_n\end{array}\right]\\ & =\sum _{i=1}^n{v}_i{a}_i\in {\mathbb{R}}^m\end{array}$$

    • and $Av$: linear combination on col. of $A$ where coeff. are provided by $v$ entries

  • example $$\begin{array}{rl}A& =\left[\begin{array}{ccc}1& 2& -1\\ 0& -5& 3\end{array}\right]\\ v& =\left[\begin{array}{c}4\\ 3\\ 7\end{array}\right]\\ Av& =4a_1+3a_2+7a_3\\ & =4\left[\begin{array}{c}1\\ 0\end{array}\right]+3\left[\begin{array}{c}2\\ -5\end{array}\right]+7\left[\begin{array}{c}-1\\ 3\end{array}\right]\\ & =\left[\begin{array}{c}4\\ 0\end{array}\right]+\left[\begin{array}{c}6\\ -15\end{array}\right]+\left[\begin{array}{c}-7\\ 21\end{array}\right]\\ & =\left[\begin{array}{c}3\\ 6\end{array}\right]\end{array}$$
  • if $A=m\times n$, then $Av$ only defined for $v\in {\mathbb{R}}^n$
    • i.e. no. of columns of $A$ should match size (rows) of $v$
    • then $Av\in {\mathbb{R}}^m$
  • $A$: transforms $\in R^n$ to $R^m$

• Linear-ness of transformation

  • transformation is linear
    1. if $A=m\times n$ and $u,v\in {\mathbb{R}}^n$ then $A(u+v)=Au+Av$
    2. if $A=m\times n$ and $v\in {\mathbb{R}}^n$ and $c\in \mathbb{R}$ then $A(cv)=c(Av)$
  • line: a spane of one vector $L=\mathbb{R}\text{-span}\{v\}$
    • then $AL:=\{Aw|w\in L\}=\mathbb{R}\text{-span}\{Av\}$
  • e.g. $\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$: counterclockwise rotation, 90 degrees

• Recap

  • linear system: can be written as vector equation as well
  • why not matrix?

• Matrix equation

  • when $A=m\times n$, $a_i,x,b\in {\mathbb{R}}^m$
  • where $x\in x$ are each variable
    • $Ax=b$: matrix equation
  • $Ax=b$: has same solution as ${\sum }_{i=1}^n{x}_i{a}_i=b$
    • and lin. sys. with augmented matrix $\left[\begin{array}{ccccc}{a}_1& a_2& \dots & a_n& b\end{array}\right]$
  • $Ax=b$: has solution $⟺$ $b$ being lin. combination of columns of $A$ $b\in \mathbb{R}\text{-span}\{a_1,a_2,\dots ,a_n\}$

• Linear systems trilogy

  • for $m\times n$ matrix $A$, following properties are equivalent
    1. for each vector $b\in {\mathbb{R}}^m$, the matrix $Ax=b$ has a solution
    2. each vector $b\in {\mathbb{R}}^m$ is a linear combination fo the columns of $A$
    3. the span of the columns of $A$ is the set $R^m$ (read: "columns of $A$ span $\mathbb{R}$")
       • same to (2), but slightly different wordings
    4. $A$ has a pivot position in every row
       • not intuitive, but computable
  • proof:
    • 1-3: different way of saying the same thing
    • 4: if $A$ has pivot in every row
      • $[Ab]$ cannot have a pivot position in the last column
      • $RREF(A)=\left[\begin{array}{cccc}1& 0& 0& \ast \\ 0& 1& 0& \ast \\ 0& 0& 1& \ast \end{array}\right]$
      • i.e. $RREF([Ab])\left[\begin{array}{ccccc}1& 0& 0& \ast & c_1\\ 0& 1& 0& \ast & c_2\\ 0& 0& 1& \ast & c_3\end{array}\right]$

• Linear independence

  • $v_i\in {\mathbb{R}}^n$ are linearly independent if the only solution to ${\sum }_{i=1}^p{x}_i{v}_i=0$
    • is $x_1=x_2=\cdots =x_p=0$
    • is there is any non-zero solution: vectors are linearly independent
  • theorem: The columns of a matrix A are linearly independent if and only if A has a pivot position in every column
  • theorem: Suppose $v_i\in {\mathbb{R}}^n$. If $p>n$ then these vectors are linearly dependent
    • $p$: no. of cols.