What is, and why probability?

probability: how likely something is to happen

• why should we learn it?
  1. randomness becomes prevalent in real life
     • e.g. revenue of Apple store at NPM next month: random
  2. probability: fundamental tool for modelling, analyzing randomness
     • e.g. what is the most likely revenue of apple store at APM next month?
  3. probability: fundamental tool for statistics, ML, etc.

Intuitions on probability

• what is the chance of selecting a red ball, among 1 green, 4 blue, and 4 red balls?
  • $\frac{4}{9}=\frac{\text{no. of reds}}{\text{no. of balls}}$
• what if we select 2 balls simultaneously?
  • what's the change that both balls are red, from 2 blue, 2 red, and 1 green balls?
  • 👨‍🎓: $\frac{2}{5}\cdot \frac{1}{4}=\frac{1}{10}$
    • 👨‍🏫: correct!

Combinations

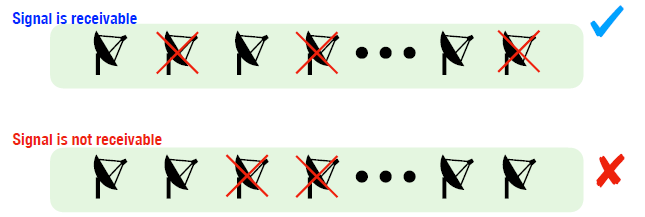
• case study: a communication system is of $n$ identical antennas in a linear order
  • the system runs as long as no 2 conseq. antennas are defective
  • and exactly $m$ out of $n$ antennas are defective
  • what is the probability that the system does not fail?
• for a special case: m=2; n=4

  • all possible config. are:

    0	1	1	0
    0	1	0	1
    1	0	1	0
    0	0	1	1
    1	0	0	1
    1	1	0	0

  • in this case: $\frac{3}{5}=\frac{1}{2}=50\%$

• for general $n,m$, the probability is
  • $=\frac{\text{no. of well-working config.}}{\text{no. of all possible config.}}$
• 👨‍🎓 programming style: can we use DP / recursion or Markov chain..?
• combinatorial analysis : mathematical theory of counting

Experiments

• experiment
  • used to denote a process whose outcome is random
  • examples
    • randomly toss a coin, roll a die, etc.
• basic principle of counting
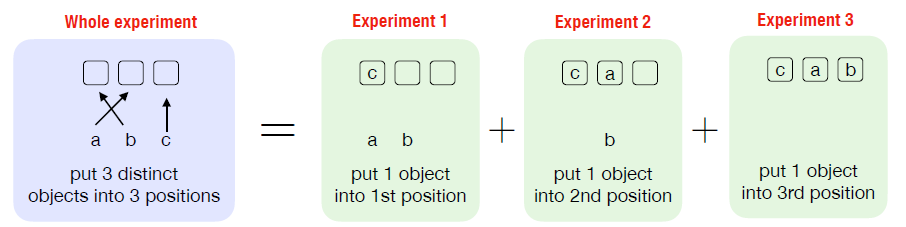
  • With two experiments performed, one resulting in any of $m$ possible outcomes , while another in any of $n$ possible outcomes , then together there are $mn$ possible outcomes of the two experiments
  • can be proved by enumerating all possible outcomes as pairs
• generalized basic principle of counting
  • With $r$ experiments performed, and $\forall i\in [1,r]$ experiment ${\text{Exp}}_i$ resulting in any of $n_i$ possible outcomes, then together there are ${\prod }_{i=1}^r{n}_i$ possible outcomes of the $r$ experiments

Permutations

• permutation: how many different (distinct) ordered arrangement of items are possible
  • 
• w/ $n$ distinct objects, the total number of different permutations are:
  • $n(n-1)(n-2)\dots 3\cdot 2\cdot 1=n!$
  • where $0!=1$ by convention
  • proof: experiment being equivalent to arrange $n$ objects into $n$ positions
• for $n$ objects which $\forall i\in [1,r]$ $n_i$ are alike, there are $\frac{n!}{{\prod }_{i=1}^r{n}_i!}$
  • proof: first compute permutation of $n$ objects
  • then. for a set of same objects, consider themselves as a (sub) permutation too
  • thus, divide it by no. of permutations that $n_i$ objects can have
• example: how many ways to rearrange the word "Mississippi"?
  • $\frac{11!}{1!4!2!4!}$ (for M, s, p, and i, respectively)

Seating in circle

• now, only the relative position matters, not linear
• to count no. of arrangements, we can first compute all "linear" permutations
  • and divide it by no. of seats (e.g. where index 0 can be located)
  • thus, there are $(n-1)!$ possible arrangements!
• if it is a necklace: $\frac{(n-1)!}{2}$ as necklace (unlike Chinese tables) can be flipped!

Introduction

• how many ways to choose $r$ items from $n$, when the order does not matter?
  • total permutation: $\frac{n!}{(n-r)!}$
  • no. of orderings: $r!$
  • no. of combination: $\frac{n!}{(n-r)!r!}$
• theorem: w/ $n$ distinct objects, no. of possible groups of choosing $r$ items are given by: $$\frac{n!}{(n-r)!r!}$$
  • also denoted by ${}_n{C}_r$ or $\left(\genfrac{}{}{0ex}{}{n}{r}\right)$
    • latter one: aka binomial coefficient
  • read "$n$ choose $r$"
• properties
  • for $r=0,1,\dots n$
    • $\left(\genfrac{}{}{0ex}{}{n}{r}\right)=\left(\genfrac{}{}{0ex}{}{n}{n-r}\right)$
  • $\left(\genfrac{}{}{0ex}{}{n}{0}\right)=\left(\genfrac{}{}{0ex}{}{n}{n}\right)=1$
  • if $r<0||r>n$: $\left(\genfrac{}{}{0ex}{}{n}{r}\right)=0$

Useful combinatorial identities

• theorem: for $1\le r\le n$:

  • $\left(\genfrac{}{}{0ex}{}{n}{r}\right)=\left(\genfrac{}{}{0ex}{}{n-1}{r-1}\right)+\left(\genfrac{}{}{0ex}{}{n-1}{r}\right)$
  algebraic proof

  $$\begin{gathered} \left(\genfrac{}{}{0ex}{}{n-1}{r-1}\right)=\frac{(n-1)!}{(n-r)!(r-1)!} \\ =\frac{(n-1)!}{(n-r-1)!(r-1)!}\frac{1}{n-r} \\ --- \\ \left(\genfrac{}{}{0ex}{}{n-1}{r}\right)=\frac{(n-1)!}{(n-r-1)!(r)!} \\ =\frac{(n-1)!}{(n-r-1)!(r-1)!}\frac{1}{r} \\ --- \\ \text{RHS}=\frac{(n-1)!}{(n-r-1)!(r-1)!}(\frac{1}{n-r}+\frac{1}{r}) \\ =\frac{(n-1)!}{(n-r-1)!(r-1)!}\frac{r+n-r}{(n-r)r} \\ =\frac{(n-1)!}{(n-r-1)!(r-1)!}\frac{n}{(n-r)r} \\ =\frac{(n)!}{(n-r)!(r)!}=\left(\genfrac{}{}{0ex}{}{n}{r}\right)=LHS \end{gathered}$$

  combinatorial proof

  • or: cheat bijections
  • $\left(\genfrac{}{}{0ex}{}{n}{r}\right)$: no. of ways of choosing $r$ no. from $1,2,\dots n$
  • count in a different ways:
    • case 1: 1 is chosen $\left(\genfrac{}{}{0ex}{}{n-1}{r-1}\right)$
    • case 2: 1 is not chosen $\left(\genfrac{}{}{0ex}{}{n-1}{r}\right)$

• theorem:

Examples

• example 1: committee
  • a committee of 3: from a group of 20 ppl
  1. how many possible committees?
     • ${}_n{C}_r{=}_{20}{C}_3=\frac{20!}{17!3!}=\frac{20\ast 19\ast 18}{6}=20\ast 19\ast 3=1140$
  2. Peter and Paul refuse to serve in the same committee; how many possibilities considering that?
     • $1140-18=1122$
     • 18: no. of committee where two guys serve together
     • alternatively: you can choose
       • when neither are in the committee + one of P & P are in committee
       • $\left(\genfrac{}{}{0ex}{}{18}{3}\right)+\left(\genfrac{}{}{0ex}{}{2}{1}\right)\left(\genfrac{}{}{0ex}{}{19}{3}\right)$
• example 2: antenna defection
  • total $n$ antenna; $m$ defective & $n-m$ functional; all functional / defective antenna are indistinguishable among them. how many linear orderings w/ no two consec. defectives?
  • procedure
    1. align functional ones in linear order
    2. and, there are $n-m+1$ spots where defectives could be located
    3. thus: $\left(\genfrac{}{}{0ex}{}{n-m+1}{m}\right)$