Introduction
information
These are my notes on MATH 2421: Probability
- Lecture 1
- Lecture 2
- Lecture 3
- Tutorial 1
- Lecture 4
- Lecture 5
- Tutorial 2
- Lecture 6
- Tutorial 3
- Lecture 7
- Lecture 8
- Lecture 9
- Lecture 10
- Lecture 11
- Lecture 12
- Lecture 13
- Tutorial 6
- Lecture 14
- Lecture 15
- Lecture 16
- Lecture 17
- Lecture 18
- Lecture 19
- Lecture 20
- Lecture 21
- Lecture 22
- Lecture 23
- Tutorial 7
- Tutorial 8
- Tutorial 9
- Tutorial 10
- Tutorial 11
- Lecture 24
Course information
- Course code: MATH 2421
- Course title: Probability
- Semester: 24/25 Fall
- Credit: 4
- Grade: A-F
- TMI
- Prerequisite: MATH 1014 OR MATH 1020 OR MATH 1024
- Corequisite: MATH 2011 OR MATH 2023
- Exclusion: IEDA 2520, MATH 2431, ELEC 2600, ELEC 2600H, ISOM 3540
Description
The course covers the basic principles of probability theory. Topics include combinatorial analysis used in computing probabilities, the axioms of probability, conditional probability and independence of events, discrete and continuous random variables; joint, marginal, and conditional densities, moment generating function; binomial, Poisson, gamma, exponential, Gamma, Beta, Cauchy, univariate, and bivariate normal distributions; laws of large numbers; central limit theorem
My section
- Section: L1 / T1B
- Time:
- Lecture: MoWe 12:00PM - 01:20PM
- Tutorial: Tu 06:00PM - 06:50PM
- Venue:
- Lecture: LG3009, Lift 10-12
- Tutorial: Rm 4580, Lift 27-28
- Instructor: WANG, Ke
- Room: Rm 3434
- Email: [email protected]
- Teaching Assistants:
- CHEONG, Kha Man ([email protected])
Grading scheme
| Assessment Task | Percentage |
|---|---|
| 5 HW | 15% |
| Mid-Term | 35% |
| Final Exam | 50% |
Required texts
- "A First Course in Probability" (8th or other Edition) by Sheldon Ross (Publisher: Prentice Hall)
Optional resources
- N/A
MATH 2421: Lecture 1
Date: 2024-09-02 03:12:22
Reviewed:
Topic / Chapter: Introduction & Principle of Counting
summary
❓Questions
- can you elaborate more on "combinatorial proof"? What is the difference between algebraic ad combinatorial?
Notes
Probability by Combinatorial Analysis: Introduction
-
What is, and why probability?
probability: how likely something is to happen
- why should we learn it?
- randomness becomes prevalent in real life
- e.g. revenue of Apple store at NPM next month: random
- probability: fundamental tool for modelling, analyzing randomness
- e.g. what is the most likely revenue of apple store at APM next month?
- probability: fundamental tool for statistics, ML, etc.
- randomness becomes prevalent in real life
- why should we learn it?
-
Intuitions on probability
- what is the chance of selecting a red ball, among 1 green, 4 blue, and 4 red balls?
- what if we select 2 balls simultaneously?
- what's the change that both balls are red, from 2 blue, 2 red, and 1 green balls?
- 👨🎓:
- 👨🏫: correct!
- what is the chance of selecting a red ball, among 1 green, 4 blue, and 4 red balls?
-
Combinations
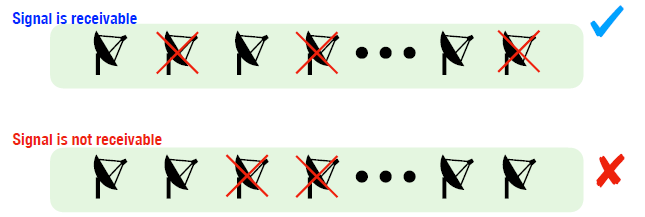
- case study: a communication system is of identical antennas in a linear order
- the system runs as long as no 2 conseq. antennas are defective
- and exactly out of antennas are defective
- what is the probability that the system does not fail?
- for a special case:
m=2; n=4-
all possible config. are:
0 1 1 0 0 1 0 1 1 0 1 0 0 0 1 1 1 0 0 1 1 1 0 0 -
in this case:
-
- for general , the probability is
- 👨🎓 programming style: can we use DP / recursion or Markov chain..?
- combinatorial analysis : mathematical theory of counting
- case study: a communication system is of identical antennas in a linear order
Principles of Counting
-
Experiments
- experiment
- used to denote a process whose outcome is random
- examples
- randomly toss a coin, roll a die, etc.
- basic principle of counting
- With two experiments performed, one resulting in any of possible outcomes , while another in any of possible outcomes , then together there are possible outcomes of the two experiments
- can be proved by enumerating all possible outcomes as pairs
- generalized basic principle of counting
- With experiments performed, and experiment resulting in any of possible outcomes, then together there are possible outcomes of the experiments
- experiment
Permutations
-
Permutations
- permutation: how many different (distinct) ordered arrangement of items are possible
- w/ distinct objects, the total number of different permutations are:
- where by convention
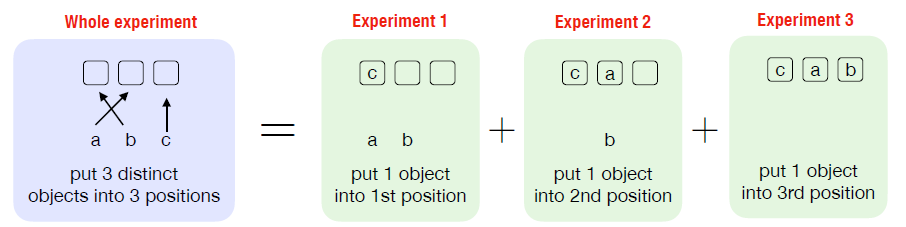
- proof: experiment being equivalent to arrange objects into positions
- for objects which are alike, there are
- proof: first compute permutation of objects
- then. for a set of same objects, consider themselves as a (sub) permutation too
- thus, divide it by no. of permutations that objects can have
- example: how many ways to rearrange the word "Mississippi"?
- (for M, s, p, and i, respectively)
- permutation: how many different (distinct) ordered arrangement of items are possible
-
Seating in circle
- now, only the relative position matters, not linear
- to count no. of arrangements, we can first compute all "linear" permutations
- and divide it by no. of seats (e.g. where index 0 can be located)
- thus, there are possible arrangements!
- if it is a necklace: as necklace (unlike Chinese tables) can be flipped!
Combinations
-
Introduction
- how many ways to choose items from , when the order does not matter?
- total permutation:
- no. of orderings:
- no. of combination:
- theorem: w/ distinct objects, no. of possible groups of choosing items are given by:
- also denoted by or
- latter one: aka binomial coefficient
- read " choose "
- also denoted by or
- properties
- for
- if :
- for
- how many ways to choose items from , when the order does not matter?
-
Useful combinatorial identities
-
theorem: for :
algebraic proof
combinatorial proof
- or: cheat bijections
- : no. of ways of choosing no. from
- count in a different ways:
- case 1:
1is chosen - case 2:
1is not chosen
- case 1:
-
theorem:
-
-
Examples
- example 1: committee
- a committee of 3: from a group of 20 ppl
- how many possible committees?
- Peter and Paul refuse to serve in the same committee; how many possibilities considering that?
- 18: no. of committee where two guys serve together
- alternatively: you can choose
- when neither are in the committee + one of P & P are in committee
- example 2: antenna defection
- total antenna; defective & functional; all functional / defective antenna are indistinguishable among them. how many linear orderings w/ no two consec. defectives?
- procedure
- align functional ones in linear order
- and, there are spots where defectives could be located
- thus:
- example 1: committee
MATH 2421: Lecture 2
Date: 2024-09-04 01:57:45
Reviewed:
Topic / Chapter: Combinations
summary
❓Questions
Notes
Combinations (cont.)
-
Useful combinatorial identities (cont.)
-
binomial theorem: let , then
- : often referred to as the binomial coefficient
- combinatorial proof
- brackets contribute , brackets for
-
-
Problems
-
how many subsets are there of a set consisting of elements?
- intuition: there are ways of choosing elements from
- alternatively: you can assign following binary values to each elements
- and there are exactly combinations!
-
show that following equation holds true
- proof (algebraic)
-
- can be shown from the previous proof
- 👨🏫 can you show combinatorial proof?
-
Multinomial Coefficients
-
Multinomial coefficients
- a set of distinct items: to be divided into different groups of respective size where
- how many divisions are possible?
- a set of distinct items: to be divided into different groups of respective size where
- alternatively:
- it's the same as arranging objects linearly ()
- and putting the first objects to group 1, next objects to group 2, etc.
- as the order doesn't matter within the set, you can divide it by and so forth
- let
- and call it multinomial coefficients
- i.e. no. of ways in dividing elements into subgroups of each size , total in
-
Theorem
- multinomial theorem
- exercise: expand
- exercise 2: expand
- multinomial theorem
-
Problems
- police department: of 10 officers
- each group: size of 5,3,2
- how many divisions exist?
- ten children: divided into team A, B of 5 groups. how many divisions?
- 10 children at playground divide themselves into teo teams of 5 each. how many divisions?
- i.e. order of team A / B doesn't matter
- police department: of 10 officers
Number of Integer Solutions
-
Theorem
- theorem: there are distinct positive integer-valued vectors that satisfies the equation
- where for
- proof: stars and bars method
- put undistinguishable stars into bins (labeled from )
- s.t. bin is empty
- let be the number of stars in the th bin ()
- it's the same as placing bars on slots (between stars)
- put undistinguishable stars into bins (labeled from )
- theorem there are distinct non-negative integer-valued vectors that satisfies the equation
- proof
-
change "non-negative" into "positive"
-
and is a positive integer
-
thus
-
- or, stars and bars method: now consider bars as objects too
- it's basically aligning stars and bars
- proof
- theorem: there are distinct positive integer-valued vectors that satisfies the equation
-
Problems
- investor: w/ 20K dollars to invest among 4 possible investment, in unit of thousand dollars.
- if the total of 20k is to be invested: how man strategies (only holding) are possible?
- 4 slots, with 20 stars
- what if not all the money need be invested?
- same as creating another investment of "nothing"
- if the total of 20k is to be invested: how man strategies (only holding) are possible?
- there are antennas with defective among them
- how many orders there exist in which no two defectives are consecutive?
- slots, bars
- 👨🏫 other approach
- .
- investor: w/ 20K dollars to invest among 4 possible investment, in unit of thousand dollars.
Axioms of Probability: Introduction
-
Recap
- Ch. 1: used intuitive definitions to calculate probability
- translated "calculate probability" into counting no. of total outcomes & no. of interesting outcomes
- however: it can't deal w/ experiments where no. of total outcome & interesting outcomes are
- we shall rigorously formalize probability
- terminologies
- random experiments outcomes
- event sample space
- rigorous definition of probability
Sample Space and Events
-
Terminology
- experiment: activity or procedure that produces distinct & well-defined possibilities
- i.e. outcomes
- basic object of probability
- sample space: set of ALL possible outcomes of an experiment
- often denoted by
- e.g. head / tail on coin tossing
- event: any SUBSET of sample space
- if random experiment produces an outcome in event
- we say "event occurs"
- if random experiment produces an outcome in event
- size of sample space / event: can be finite or infinite
- experiment: activity or procedure that produces distinct & well-defined possibilities
MATH 2421: Lecture 3
Date: 2024-09-09 12:46:15
Reviewed:
Topic / Chapter: Event Operations and Probability
summary
❓Questions
- why do we need to use infinity in defining probability when we can use the concept of exhaustive events?
- 👨🏫 They (use of or ) are equivalent and it's matter of personal preference.
- We have used infinity version to follow the textbook
Notes
Operations on Events
-
Four basic operations
- result of operation: also a collection of outcome = event
- union:
- either event or event occurs
- intersection:
- both event and event B occur
- short:
- complement:
- even A does NOT occur
- symmetric difference: \
- EITHER or occurs, but not both
-
Additional terms
- inclusion of events
- or
- i.e. occurrence of implies
- disjoint
- when two events share no common outcomes
- mutually exclusive
- when events are pairwise disjoint
- exhaustive
- when union of some events is the sample space
- partition
- when events are both exclusive and exhaustive
- and
- inclusion of events
-
Fundamental laws
- commutative law
- associative law
- distributive law
- DeMorgan's law
- commutative law
-
Lemma
- for any events :
- proof: as above is
- following distributive law
- proof: as above is
- for any events :
Axioms of Probability
-
Probability definition
- probability: function that assigns numbers to events
- numbers: characterize how likely this event occurs
- primitive definition
- assuming an experiment w/ sample space can be repeated
- for each even , : number of times occured in the first repetitions
- probability is defined by:
- l.e. limiting proportion of time that occurs
- problems
- how do we know the limit of exists or not, for a seq. of repetitions?
- even if limits exist for all sequences, how do we know that the limits are the same = i.e. converge?
- Kolmogorov Axiom (modern probability definition)
- by Andrey Kolmogorov in 1933
- probability, denoted by is a function on the collection of events satisfying
- for any event :
- let be the sample space, then:
- for any sequence of mutually exclusive events
- also written as, for all
- event
- probability: function that assigns numbers to events
-
Example
- on a fair six-faced dice, when ,
- by Kolmogorov's axiom, what are and ?
- as each faces are mutually exclusive (cannot have two or more faces at once)
- on a fair six-faced dice, when ,
Properties of Probability
-
Theorem
-
- proof: take ,
- are mutually exclusive
- by axiom 3:
- for any finite sequence of mutually exclusive events
- proof: let
- : still mutually exclusive
- apply axiom 3 to find:
- let be an event, then
- proof:
- if , then
- proof:
- since
- by Axiom 3,
- let be any two events, then
- proof by diagram

- rigorous way
- : disjoint
- using axiom 3:
- since , : disjoint
- using axiom 3:
- Inclusion-Exclusion principle
- let be any events, then:
- where means sum of every possible combination of
- 👨🏫 won't be used for
- let be any events, then:
-
-
Example
- let two events s.t. f
- and . find
- J is taking two books for vacation.
- : reading first book;
- : reading second book;
- what is
- formula for
- or, consult diagram for easy understanding
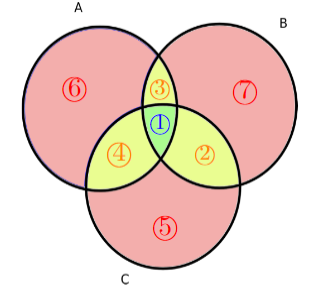
- or, consult diagram for easy understanding
- let two events s.t. f
MATH 2421: Tutorial 1
Date: 2024-09-10 17:17:12
Reviewed:
Topic / Chapter: Exercises
summary
❓Questions
Notes
Introduction to Tutorial
- Instructor: TA CHEONG, Kha Man
- Feel free to attend different section's tutorial!
Exercises
-
Problem 1 (permutation)
- Five people, designed as A, B, C, D E, are arranged in linear order.
- How many ways to arrange these five people?
- ways
- How many ways to arrange these five people, if they are arranged in a circle?
- as you can rotate the same combination into five different order:
- ways
-
Problem 2 (permutation)
- How many different ways can 3 red, 4 yellow and 2 blue bulbs be arranged in a string of Christmas tree lights with 9 sockets?
- 1260 ways?
-
Problem 3 (combinations)
- A committee of 5 people is to be chosen from a group of 6 men and 4 women. How many committees are possible if
- there are no restrictions?
- 252 ways
- one particular person must be chosen on the committee?
- there are to be 3 men and 2 women?
- 120 ways
- there is to be a majority of women?
- either: 3 woman or 4
- 3 women:
- 4 women:
- 60+6=66 ways
-
Problem 4 (combinations)
- If 4 Maths books are selected from 6 different Maths books, and 3 English books are selected from 5 different English books, how many ways can the seven books be arranged on a shelf (linear order):
- if there are no restrictions?
- if 4 Maths books remain together?
- one for arranging 4 "groups" (3 individual English books, and 1 group of math books)
- and another for order within the math books
- if Maths and English books alternate?
- if a Math book is at the beginning of the shelf?
MATH 2421: Lecture 4
Date: 2024-09-11 12:02:33
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Sample Spaces Having Equally Likely Outcomes
-
Assuming Equally-Likely
- for many experience: natural to assume all outcomes in finite sample space: equally likely to occur
- e.g. fair coin / die
- notation
- ; or
- then, follows from Axiom 3 that, for
- for many experience: natural to assume all outcomes in finite sample space: equally likely to occur
-
Examples
- trump cards
- assuming all 52 cards in a deck is equally likely to occur
- and : drawing diamond; : drawing Jack
- what is
- drawing random balls
- if 3 balls are randomly drawn from set of 6 white and 5 black balls
- what's probability that one of the drawn balls is white
- and the other two black?
- 3 ordering possible
- total ways:
- alternatively
- no. of choosing 1 white and 2 black:
- birthday problem 2
- how large must the group be, so that there is a probability io greater than 0.5, that someone will have the same birthday as your do?
- exclude Feb 29 for calculation; assume unifom distribution
- s.t.
- // switch side
- birthday problem 1
- what is the probability that in a group of people, at least of the will have the same birthday?
- or:
- and as when is small
- as
- trump cards
Conditional Probability and Independence: Introduction
-
Why conditional probability
- We can leverage the information we have!
Conditional Probability
-
Definition
-
- ⭐conditional probability:
- read: given that has occurred
- if , then
- if , then
- (simple notation change)
- ⭐ by Kolmogorov's axioms, is a valid probability?
- check
-
- true as
-
- true as (as )
- holds as are mutually exclusive to one another
-
- thus, is a valid probability
- and therefore properties of probability holds for , such as:
- check
-
-
Examples
- if we know that event has occurred
- then , not !
- suppose 2 fair dice are are rolled
- and we observe that the first die is a
- given that, what is the probability that the sum of 2 dice equals 8?
- i.e. second die = , so
- or:
- student: taking 1-hr exam
- suppose : student will finish exam in less than hours: ()
- given that student: still working after hrs ()
- what's the conditional probability that the full hour will be used? ()
-
- 80%
- if we know that event has occurred
MATH 2421: Lecture 5
Date: 2024-09-16 12:03:51
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Conditional Probability (cont.)
-
Theorems
- multiplication rule
- if , then
- general multiplication rule
- for events
- 👨🎓 more like, nested use of multiplication rule
- explanation
- and cancel, cancel
- or, as mentioned above, nested use
- multiplication rule
-
Examples
- bin: with 25 light bulbs
- A: 5: good & functional for more than 30 days
- B: 10: partially defective; fail in the second day of use
- C: rest: totally defective
- if: a random bulb initially lights up ()
- what is the probability of it working after 1 week? ()
- Celine: chance of getting A in French, and chance for chemistry
- is her decision: based on fair coin
- what is the chance that she gets an A in chemistry?
- Celine getting A
- Celine taking chemistry
- suppose: an urn w/ 8 red balls & 4 white balls
- we draw 2 balls, one at a time, without replacement
- assuming fair chance, what is the probability that both balls drawn are red?
- w/ conditional probability
- first ball drawn: red
- second ball drawn: red
- w/ combinatorial analysis
- i.e. counting no. out interested outcomes / all possible outcomes
- no. of choosing 2 red balls / no. of choosing arbitrary balls
- three cards: selected successively at random, without replacement
- 52 playing cards
- calculate probability of receiving in order: K,Q, and J
- conditional probability
- combinatorial analysis
- no. of outcome w/ K-Q-J / no. of total outcomes
- box of fuses w/ 20 fuses
- 5 are defective
- 3 fuses: selected randomly and removed from all
- what's the probability that all 3 are defective?
- conditional probability
- combinatorial analysis
- If six cards are selected at random (without replacement) from a standard deck of 52 cards, what is the probability there will be no pairs?
- conditional probability
- each turn:
- combinatorial analysis
- conditional probability
- bin: with 25 light bulbs
Total Probability
-
Introduction
- how can we compute probability under different conditions / cases?
- e.g. probability of getting 3 on a fair die
- case 1: 4-faced fie is chosen:
- case 2: 6-faced fie is chosen:
- assuming both cases happen with equal chance
-
Theorem
- let be any two event, then
- 👨🏫 or: prob. of occurs = weighted average of the conditional probabilities of
- conditioning on either occurs or does not occur
- proof: w/ Venn diagram
- ,
- partitions the sample space if:
- they are mutually exclusive:
- they are exhaustive:
- law of total probability
- if partitions the sample space and
- let B any event, then
-
- proof:
- because
- because
- proof:
- let be any two event, then
-
Examples
- MCQ exam
- a student: either knows the answer at probability , or guesses at probability
- there are alternatives
- what is the probability that he answered it correctly?
- : student knows;
- : student guesses:
- : student answers correctly
- what is the probability that the student knew the answer, given that he answered it correctly?
- 👨🏫 aka: Bayes formula
- Insurance company: categorizes people into 2 groups: accident-prone and others
- accident-prone person: will have accident in a fixed 1 yr time with probability of 0.4
- 0.2 for others
- if 30% of population is accident prone, what's the change that new policyholder will have an accident within an year?
- : person being accident prone
- : person having accident in 1 year
- accident-prone person: will have accident in a fixed 1 yr time with probability of 0.4
- party support
- 40% of people support party , 30% , 20% , 10%
- : certain policy
- 50% of supporter supports it
- 40% of supporter supports it
- 30% of supporter supports it
- 100% of supporter supports it
- what is the probability that a random citizen supports the policy?
- MCQ exam
Bayes' Theorem
-
Introduction
- if partitions the sample space
- and
- then, for any
- proof:
- and expand the denominator
- if partitions the sample space
MATH 2421: Tutorial 2
Date: 2024-09-21 22:25:32
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Tutorial 2
-
Properties of Probability
- 60% of students: wear neither a ring / necklace
- 20% wears ring; 30% wear a necklace
- what is the probability of student wearing
- a ring / necklace?
- a ring & necklace?
-
Sample Spaces Having Equally Likely Outcomes
- Five people, designated as A, B, C, D, E, are arranged in linear order. Assuming that each possible order is equally likely, what is the probability that
- there is exactly one person between A and B?
- there are exactly two people between A and B?
- there are three people between A and B?
-
Conditional Probability
- from years of production: of robots are defective.
- if robot is not defective, it tests negative for 97% of time
- if robot is defective, it tests positive for 99.5% of time
- probability that a randomly selected robot: negative result?
- : event of being tested positive
- : event of actually being defective
- probability that a randomly selected robot is defective, given positive result?
-
General Multiplication Rule
- deck of 52: divided randomly into 4 distinct piles of 13 cards each
- probability that each pile: has exactly 1 ace?
-
Inclusion-Exclusion Principle
- Suppose that there are distinct types of coupons and each time one obtains a coupon it is, independent of prior selections, equally likely to be any one of the types. Denote as the number of distinct types of coupons that are contained in the first selections. Find .
- probability that distinct tickets :
- no. of ways to choose types * no. of ways to choosing tickets within / total ways of choosing tickets within
- must be multiplied by in order to be correct.
- let : no empty category exists within
- : empty slot
- : -th slot is empty
- final answer:
MATH 2421: Lecture 6
Date: 2024-09-23 11:41:56
Reviewed:
Topic / Chapter: Bayes theorem & independence
summary
❓Questions
Notes
Bayes' Theorem
-
Bayes' theorem
- given partitions
- and for all
- and any event, then:
- proof
- then: law of total probability
- terminology
- prior probability
- : evidence
- posterior probability
- given partitions
-
Examples
- I saw a mule!
- but it is surely mistaken, as there are only horse and donkey in the village.
- there are 30% horses and 70% donkeys
- prior belief: there is 30% chance to encounter a donkey
- if: horse is mistaken as a mule w/ 0.4
- and donkey is mistaken w/ 0.8
- then
- then
- Covid tests
- PCR test vs. RAT
- different cases:
- : sick people correctly identified as sick
- : healthy people incorrectly identified as sick
- : healthy people correctly identified as healthy
- : sick people incorrectly identified as healthy
- terminology
- sensitivity:
- i.e. probability of a positive result given patient: is sick
- specificity:
- i.e. probability of a negative result given patient: is healthy
- : prob. of
- prevalence:
- sensitivity:
- prevalence of covid: 1%
- test: w/ sensitivity 95%
- specificity: 99%
- test result: positive
- probability that you have covid?
- test: w/ sensitivity 95%
- class exercise
- if 5% or 8%, how does change?
- how about ?
- class exercise 2
-
- 👨🏫 sensitivity & specificity matter much, esp. it's multiplied twice
-
- blood type
- 95% effective in detecting a disease when it is present
- false positive: 1% for healthy person
- prevalence: 0.5%
- plane: missing
- equally likely: in 3 possible regions
- : plane is in region =
- : probability that plane: found upon search in -th region
- when plane is indeed there
- : search in region 1: unsuccessful
- = plane not found in region 1 upon search
- for
-
- for each
-
-
-
-
- 👨🏫 less chance of unsuccessful search, if the plane is actually there!
-
-
-
- equally likely: in 3 possible regions
- assembly plant w/ 3 machine types
- each is of proportion: 30% / 45% / 25%
- and defective rate: 2% / 3% / 2%
- given a chosen machine is defective, what is the probability of it being type 1?
- I saw a mule!
Independence
-
Independence
- two events : independent if
- ⭐
- and dependent if
- motivation: if , then
- i.e. : independent of if
- knowledge that has occurred: does NOT change the probability that occurs
- if are independent, then so are:
- 👨🏫 and similarly for others
- two events : independent if
-
Examples
- card: selected at random from ordinary deck of cards
- if : event that selected card = Ace
- : is is spade
- then : independent
-
- thus they are independent
- 👨🏫 they are not disjoint (i.e. ), but they are independent
- two coins: flipped
- all 4 outcomes: equally likely
- : first coin lands head
- : first coin lands tail
- another two fair coins
- : first coin lands head
- : only one coin lands head
- 2 fair dice
- : sum of dice = 6
- : first die = 4
- are independent?
- 2 fair dice
- : sum of dice = 7
- : first die = 4
- are independent?
- card: selected at random from ordinary deck of cards
MATH 2421: Tutorial 3
Date: 2024-09-24 18:06:07
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Tutorial
-
Tutorial
- evens are independent if: for every sub-collection
- and meaningful sub-collection: must have elements
- i.e.
- all subset - no. of individual events - empty set
- evens are independent if: for every sub-collection
Exercises
-
Independent events
- each independently component: function at prob.
- that is the prob. that any of component works?
- as, for independent events,
- Solution:
- 👨🏫 or, more simply:
- let : system functions
- ans : component functions
- let : system functions
-
Bayes' theorem
- 3 types of flashlight
-
- a) ?
- sum of products:
- b) for ?
- 3 types of flashlight
-
Month Hall problem
- 1 car and 2 goats
- you can choose a door,
- after your choice, the host removes one door with a goat behind,
- then, does changing the door make you more likely to get the car?
- let probability that car is behind it
- let probability that door was opened
- // no other box to open
- thus: better to change
-
Random Monty Hall problem
- What if the host opens a door that we did not pick, but which might contain car?
- 1/2
MATH 2421: Lecture 7
Date: 2024-09-25 12:07:25
Reviewed:
Topic / Chapter:
summary
❓Questions
- ❓ can we say is independent of itself?
- 👨🏫 only if
Notes
Independence (cont.)
-
Independence (cont.)
- three events: independent iff:
- last three: pairwise independent
- if independent => independent of any objects formed of
- as:
- as:
- events are independent, if:
- sub-collection of
-
- for
-
- for , verify:
- ; condition
- ; conditions
- and similarly so one
- ; conditions
- // pairwise independent
- ; condition
- sub-collection of
- three events: independent iff:
-
Examples
- two fair dice: thrown
- : sum of dice = 7
- : first dice = 4
- : second dice = 3
- yet
- dependent on
- : sum of dice = 7
- loaded coin w/
- loaded coin: tossed times
- probability of getting at least 1 head in these tosses?
- probability of getting exactly head in these tosses?
- if first tosses: give heads
- remaining tosses: all tail
- event:
- and there are ways to choose it
- thus final solution:
- if first tosses: give heads
- system: of independent components
- is parallel if it functions when at least one component functions
- if component functions in
- then what is the probability that the system functions?
- two fair dice: thrown
Random Variables: Def. of Random Variables
-
Introduction
- Need for random variable
- often: we are interested in some function / expression of outcome
- rather than outcome itself
- e.g. roll a pair of dice; what is the distribution of two faces' sum?
- i.e. not interested in face of each die
- function:
- range:
- 20 questions in a MCQ. Each question w/ 5 alternatives
- student: answers all 20 questions randomly
- independently choose one alternative in each questions
- interested in: no. of correct answers
- Need for random variable
-
Random variables
- random variable: mapping from sample space to real numbers
- rv: random variables
- denoted by capitals,
- discrete random variable
- rv w/ finite || countable range
- e.g. number of defective items
- continuous random variable
- range: an interval over the real line
- weight of an item, time taken, etc.
- random variable: mapping from sample space to real numbers
-
Examples
- urn: w/ 20 chips w/ number
- three chips: chosen at random
- : largest among the three chips
- then, what's the range of ?
- (discrete)
- toss 3 coins. : no. of heads appearing
- (discrete)
-
- partition of
- from above urn, compute the probability of
-
- choose , and 2 other that is smaller that
- i.e. within
- three balls: randomly chosen from urn w/ 3W, 3R, 5B balls
- we win 1 per R ball chosen.
- : total winnings of the experiment
- compute respective probability for all domain of
- and
- probability of winning money
- urn: w/ 20 chips w/ number
Discrete Random Variables
-
Discrete random variables
- rv: discrete if range of : either finite / countably infinite
- using: capital for variable
- and for value
- suppose rv is discrete, taking value of
- probability mass function of , is
- for PMF: range must be well-determined
- PMF: fully characterizes a rv
- can be notated as
- probability mass function of , is
- properties of PMF
- for
- for other values of
- domain of pMF itself: entire real line
- ⭐ since must take on one of the values of
- rv: discrete if range of : either finite / countably infinite
-
Examples
- rv : only takes value if is of the form
- where : fixed positive value; : suitably chosen constant
- : also known as a normalizing constant
- a) what is this suitable constant
- as
-
- Taylor series
- 👨🏫 sometimes, is almost impossible to calculate
- b) compute
- c) compute
- rv : only takes value if is of the form
MATH 2421: Lecture 8
Date: 2024-09-30 11:59:52
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Discrete Random Variables
-
Cumulative distribution function
- cumulative distribution function: or d.f. of :
- for
- like pmf: cdf fully characterizes random variable
- for discrete , : a step function
- taking jump of upon reaching it
- for
- then constant in
- to know cdf, knowing pdf of following range is enough
- ⭐ more properties of CDF (in general)
- : monolithic / non-decreasing
- always starts at / near 0 for small
- and end at or near for large
- discrete r.v.'s cdf: a step function
- : right-continuous
- i.e. can approach the limit only from the right
- cumulative distribution function: or d.f. of :
-
Examples
-
if w/ pmf by
- then cdf:
-
- jump of
-
- jump of
-
- jump of
-
- jump of
-
no. of mortgage approved per week: given below
approved 0 1 2 3 4 5 6 probability 0.1 0.1 0.2 0.3 0.15 0.1 0.05 - prob: fewer than 4 mortgage approved
- prob: more than 2, but no more that 5 approved
- or:
- cdf chart: trivial
- prob: fewer than 4 mortgage approved
-
given cdf, show pdf
- simply by
- and
0 1 2 3 4 5 6 0.1 0.1 0.2 0.3 0.15 0.1 0.05
-
Expected Values
-
Expected value
- expectation or expected value of discrete random var :
- aka
- : a random var
- but : a deterministic number
- i.e. a weighted average over all possible value
- and some of weight: 1
- usually: we use for r.v. (as they are functions)
- and for the values
- interpretations of expectation
- weighted average of possible values of
- weight:
- measure of central location of r.v.
- expectation of average val of r.v. over large no. of experiments
- further connected w/ ch. 8: law of large numbers
- weighted average of possible values of
- expectation or expected value of discrete random var :
-
Example
- suppose: only takes only 0 / 1
- and and
- random variable: called Bernoulli r.v. of parameter
- denoted by
- expected value of a fair 6-face die:
- i.e.
- newly wed couple: continue to have children until they have 1 of each sex
- if: boy-girl chance are independent & equally likely
- then how many children should this couple expect?
- assume: get sex 1 for first try
- and let : no. of tries until getting sex
- prof's way
- : prob. that first children are girls, and then boy
- compute
- and, from calculus:
- if
-
- derivation
- as ,
- suppose: only takes only 0 / 1
Expectation of a Function of a Random Variable
-
Expectation of value
-
if
- then
-
given and function , how can we compute ?
- standard: compute pmf of , and compute by definition
- alternatively: you can break it down
- in general:
- 👨🏫 no need to compute pmf for separately
- standard: compute pmf of , and compute by definition
-
theorem: r.v. w/ value for for
- then for any real value function
-
proof:
- idea: group together all terms in w/ same value for , then represent it as sum per each distinct value of
-
- is called a second moment of
- for : called k-th moment of
-
let then
- (notation)
- is called -th central moment
-
remarks
- : aka first moment / mean of
- first central moment:
- second central moment:
- aka variance of
-
let : constants, then
- 👨🏫 expectation: a linear operator
-
proof:
-
MATH 2421: Lecture 9
Date: 2024-10-02 12:08:29
Reviewed: 2024-10-07 16:01:23
Topic / Chapter:
summary
❓Questions
Notes
Expectation of a Function of a Random Variable (cont.)
-
Expectation of value
- for non-negative integer-valued r.v.
- tail sum formula fo expectation
- proof
- for non-negative integer-valued r.v.
Variance and Standard Deviation
-
Variance & standard deviation
- for random variable w/ mean , variance is given by:
- i.e. measure of scattering / spread of the values of
- standard deviation of or :
- proof:
- w/ discrete r.v.,
- remarks
- as it's squared
- iff is a degenerate r.v.
- i.e. taking only one value: mean
- special case of some inequality
- following tha formula:
- proof
-
- similarly, just
sqrtat each side
- similarly, just
- for random variable w/ mean , variance is given by:
-
Problems
-
calculate is : outcome when a fair die is rolled
-
consider the prob. distribution on stock
- find expected return:
X Y prob A return B return 0.2 1% 10% 0.3 2% 6% 0.3 3% 2% 0.2 4% -2% - find variance & SD of return
-
Discrete Random Variables arising from Repeated Trials
-
Modeling repeated trials
- repeating
- each trial results in an event, or not
- occurrence of event: success
- non-occurrence of event: failure
- each trial w/ success probability , failure with
- repeating trials independently
- such trial: Bernoulli (p) trials
- Bernoulli random variable
-
performing experiment only once:
- ,
- ;
- as
-
denote by
-
aka
-
aka
-
aka
-
distribution of Bernoulli r.v.: Bernoulli distribution
-
- Binomial r.v.
- experiment times and define
- no. of success in trials
- denoted by
- binomial r.v., Binomial distribution
- is it a valid pmf?
- i.e. show
- experiment times and define
- if then ,
- proof on
- proof on
- geometric random variable
- let : no. of trials to obtain the first success
- and
- and
- denoted by
- calculus tools
- for
- for
- for
- proof on
- 👨🏫 show the variance one yourself!
- another version of geometric distribution
- : no. of failures in trials
- in order to obtain the first success
- and
- for
- conventionally: geometric seq. means (at least in this course)
- : no. of failures in trials
- negative Binomial r.v.
- : no. of to get success
-
- 👨🎓 better:
- denoted by:
- 👨🏫 it's called negative binomial, because it is extended from negative binomial theorem
- or:
- repeating
MATH 2421: Lecture 10
Date: 2024-10-07 12:02:15
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Discrete Random Variables arising from Repeated Trials (cont.)
-
Practice
- gambler: makes seq. of 1 dollar bets on black
- success: winning 1
- wins if ball stops on one of positions
- lose otherwise
- in small town: out of 12 accidents, at least 4 happened on Friday 13th
- does it mean that Friday 13th seems to be auspicious?
- suppose: probability accident to occur on Friday 13th: same as other days
- then, probability of four or more accidents on Friday the 13th:
- such rare probability; good reason to believe so (hypothetically)
- geometric distribution: plays important role in theory of queues
- e.g. line of customers
- assume: each small time unit, either 0 or 1 new customers arrive
- probability that a customer arrive: , not arriving:
- time until next arrival: has a geometric distribution
- what is the probability no customer arrives in next time units?
- i.e.
- or: no success in sequence of consecutive time units
- thus
- 10 students: randomly pick one number from
- let : r.v. on number of students who picked no. 8
- find the probability: more than 1 student pick no. 8
- no. of success in 10 trials
- communication system w/ components
- each: function w/ probability , independently
- total system: operate effectively if at least one-half of components function
- for what values of : 5-component system works better than 3-component?
- : number of components working in -component system
- given
- gambler: makes seq. of 1 dollar bets on black
Poisson Random Variable
-
Poisson Random Variable
- ⭐ r.v. : Poisson distribution w/ parameter
- if for
- for
- if for
- defines: probability mass function
- notation:
- theorem: if ,
- Poisson random variable: tremendous range of applications
- for determining probability of counts over time
- example
- no. of traffic accidents occurring on a highway in a day
- crashes of a computer network per week
- no. of people joining a line in an hours
- no. of customers per day
- no. of goals in a hockey game
- no. of typos per page of an essay
- Poisson random variable: can be used for approximation for binomial r.v. w/ parameter
- if is larger is small enough
- i.e. : moderate size
- suppose binomial r.v. w/ and
- then
- no. of successes in trials
- law of rare events: if is large and is small
- then
- ⭐ usually if and
- remarks
- w/ independent trials w/ success probability
- when is large and small for moderate
- no. of success occurring: Poisson random
- examples
- no. of misprints on a page
- no. of people in community living to 100 yearsno. of wrong telephone no. that are dialed in a day
- no. of people entering a store on a given day
- with large , above and many others become approximately Poisson
- if is larger is small enough
- on units on time and rate occurrences per unit time, then
- : r.v. of count of occurrences of even over period of time
- proof: non trivial
- ⭐ r.v. : Poisson distribution w/ parameter
-
Problems
- which of following r.v. has infinite range?
- answer: Poisson
- Be:
- Bin:
- Poisson:
- suppose: no. of typographical errors on a page: w/ Poisson distribution
- parameter:
- calculate prob. there exists at least one error on a page
- suppose: probability of an item produced by a machine w/ defective rate
- find: probability that sample of 10 samples: contain at most 1 defective item
- : no. of defective items among 10 samples
- w/ Poisson approximation:
-
- 👨🏫 pretty close!
- suppose: during a particular minute of day
- people: serviced in a particular telephone service area
- independently decide whether to place an emergency call
- w/ probability
- and let : actual random no. of 911 callers in that minute
- find:
-
- 👨🏫 don't try to run it on calculator!
- approximating:
- during lab experiment: average no. of radioactive parties passing counter per 1 ms: 4
- given no. of particles passing follows a Poisson distribution
- what is the probability that 6 particles enter the counter in a given ms?
- : no. of passing through counter in 1 ms
-
- 👨🎓 and, for Poisson,
- studying earthquakes in California
- w/ reading over 6.7 on Richter scale
- on average: 1.5 earthquakes w/ such condition per year
- : rate of the occurrence of earthquakes
- let : rv of number of earthquakes above 6.7 in upcoming year, then
- probability that there will be 5 earthquakes w/ reading over 6.7
- in upcoming year:
- in next 4 years:
- on units on time and rate occurrences per unit time, then
- : r.v. of count of occurrences of even over period of time
- 👨🎓 6 in next 4 years:
- in upcoming year:
- average no. of homes solve by agency: 2 homes / day (Poisson)
- what is the probability that exactly 10 homes will be sold by agency in the next 30 days?
- which of following r.v. has infinite range?
Hypergeometric Random Variable
-
Hypergeometric Random Variable
- suppose: w/ set of balls, w/ red balls and blue balls
- and choose: of such balls without replacement
- : no. of red balls in sample
- for
- random variable w/ PMF given as above: hypergeometric r.v.
- denoted by:
- suppose: w/ set of balls, w/ red balls and blue balls
MATH 2421: Lecture 11
Date: 2024-10-09 12:02:10
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Hypergeometric Random Variable (cont.)
-
Practice
- purchaser of electrical component: buys in lots of size 10
- policy: inspect 3 from a lot
- and all must be non-defective
- w/ 30% of lots having 4 defective components
- and 70% w/ 1 defective component
- what proportion of lots: does purchaser reject?
-
-
- purchaser of electrical component: buys in lots of size 10
Expected Value of Sum of Random Variables
-
Expected value of sum of random variables
- 👨🏫 more discussion in Ch. 7; important!
- for a r.v. , let : val. of when being output
- if : both r.v. their sum is also r.v.
- : also r.v.
- r.v.: map from sample space to real line
- theorem: let : probability that : output of experiment
- then
- proof
- suppose, for distinct values of are
- for each : : event
- i.e.
- ⭐ linearity of expectation
- for r.v. (no independence req.)
- proof
-
Practice
- suppose: experiment consists of flipping a coin 5 times
- result: only heads & tails
- : no. of heads in first 3 flips
- : no. of heads in last 2 flips
- then - for any combination
- suppose: two independent flip of a coin
- head w/ probability of maid
- : no. of heads obtained
- thus
- as well as
- find: expected total no. of success from trials
- when trial : success w/ probability
- let
- special case: and trials independent:
- then
- identical & independent trials
- each trial: yields success w/ same
- if success
- proof
- show:
- by def. : total no. of success in independent
- thus
- ⭐⭐ w/ same , then always
-
- where
- and all independent
-
- each trial: yields success w/ same
- for
- suppose: experiment consists of flipping a coin 5 times
Continuous Random Variables: Introduction
-
Continuous r.v.
- r.v. w/ range being an interval over real line
- weight / time / length ...
- considered separate as:
- 👨🏫 you can't get exactly 30 cm long ruler, etc.
- for a continuous r.v.
- and thus
- and
- for cont. r.v. , w/ property s.t.
- : non-negative function,
- then: : probability density function (pdf)
- for all
- as:
- distribution function (cdf): defined by
- 👨🏫 same as discrete!
- w/ fundamental theorem of calculus:
- density: derivative of cumulative distribution function
- (think of it as a area of small slice of rectangle)
- : measure of how likely that r.v. will be near
- probabilities
- r.v. w/ range being an interval over real line
MATH 2421: Lecture 12
Date: 2024-10-14 11:50:44
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Continuous Random Variables: Introduction (cont.)
-
Continuous r.v. (cont.)
- remarks
- for cont. r.v.
- : continuous
- simple facts
- determining constant in PDF
- remarks
-
Problems
- for a cont. r.v. w/ following PDF:
- compute value of
- compute value of
- electrical appliance: function for a random amount of time
- exponential distribution
- CDF:
- value of ?
- for any ,
- property s.t.
-
- i.e. memoryless property
-
- lifetime in hour of a radio tube: given by
- what is the probability that exactly 2 of 5 such tubes: have to be replaced within first 150 hours?
- desired property
- for a cont. r.v. w/ following PDF:
Expectation and Variance of Continuous Random Variables
-
Expected value and SD
- theorem
- for any real value function
- ⭐⭐
- then same linearity, variance, or variance of linear function
- theorem: tail sum formula
- for a nonnegative continuous random variable
- proof
- theorem
-
Problems
- find the mean and variance of the random variable
- : uniform distribution over
- find w/ of following pdf
- stick of length 1: broken at random
- determine expected length of the piece containing point of length from one end ()
- when is fixed
- let : break point, then length denoted by :
- if then
- else:
- finding:
- upon meeting: being minutes early costs you
- while being late minutes cost
- suppose: traveling time is a cont. r.v. given by
- if , given by
- if : 0
- determine: what time to depart in order to minimize cost
- suppose: you leave minutes before the appointment
- step 1: find expected cost
- step 2: minimize
- let be the cost
- expected value:
- minimizing (finding optimal value, etc.)
- recall that:
- and
- thus
-
- if : w/ absolute minimal at
- find the mean and variance of the random variable
MATH 2421: Lecture 13
Date: 2024-10-21 11:56:40
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Uniform Distribution
-
Uniform distribution
- : uniformly distributed aver the interval if pdf is given by:
- denoted by:
- every neighbor: equally likely
- CDF:
- similarly shows that: ,
- : uniformly distributed aver the interval if pdf is given by:
-
Problems
- buses: arrive at stop on 15-min intervals from 7:15 am
- passenger: arrives at stop uniformly at random time between .
- find probability: the man arriving in less that 5 mins after arrival
- i.e.
- find probability: the man arriving more than 10 minutes late
- 👨🏫 exercise!
- buses: arrive at stop on 15-min intervals from 7:15 am
Normal Distribution
-
Normal distribution
- : normally distributed w/ parameters , pmf given by:
- notation:
- density function: bell-shaped, always positive. symmetric on and peaks at
-
Standard normal r.v.
- , pdf: , cdf:
- theorem: for ,
- note: don't try to evaluate cdf of general normal distribution by hand
- simple impossible :p
- some intuitions
- bell curve's left half: same size as right
- total area / region: 1
- for ,
- properties of the standard normal
- (aligned by center)
- (symmetric)
- for
- for
- ⭐ if . then
- ⭐ if . then for
- 👨🏫 more generally: linear transformation of a normal r.v. is still a normal r.v.
- -th quantile of a r.v. : s.t.
- for ,
- , pdf: , cdf:
- Problems
- when , compute
- width of a slot of duralumin in forging: normally distributed with
- specification limits:
- what percentage of forgings will be defective?
- what is the maximum allowable value of to permit no more than 1 in 100 defectives, when ?
- ,,
- when , compute
MATH 2421: Tutorial 6
Date: 2024-10-22 18:08:37
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Tutorial 6
-
Tutorial
- exponential distribution
- if , then
- , ,
- memoryless property:
- 👨🏫 : waiting time for first arrival
- shares the parameter with Poisson distribution
- as expected time to wait:
- if , then
- exponential distribution
-
Exercises
- continuous r.v.
- for some constant , pdf of is:
- find ,
- when , find and
- normal dist.
- total sales: follow normal distribution
- ,
- probability: firm's sale fall within 150,000 of the mean?
- determine: sales level w/ 9% of being exceeded next year
- normal dist.
- weights of kindergarten students:
- find probability: exactly randomly selected students weigh less than
- and
- exponential dist.
- : exponential r.v. w/
- show:
- Chi-squared dist.
- if , find pdf of
-
- pdf of times two, as two exists with same probability
- continuous r.v.
MATH 2421: Lecture 15
Date: 2024-10-28 11:58:17
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Function of a Continuous Random Variable (cont.)
-
Theorem
- theorem: w/ being cont. r.v. having pdf
- suppose: strictly monotonic, differentiable function of
- 👨🏫 i.e. inverse function exists
- then r.v. has pdf given by
- : value of s.t.
- suppose: strictly monotonic, differentiable function of
- proof
- assume: increasing
- and same for
-
- and, from chain rule:
- ⭐
- and, as non-decreasing, its derivative is non-negative
- when , either or : leading to
- and, from chain rule:
- assume: increasing
- Remarks: if cont. r.v. w/ strictly increasing cdf
-
- thus, we can perform inverse transformation method
- generating cont. r.v. w/ distribution from
- , then
- theorem: w/ being cont. r.v. having pdf
-
Example
- let , find cdf, pdf. of
- if :
- if
- actually
- aka Chi-squared distribution
- same , , aka lognormal r.v.
- define pdf
- for ,
- else:
- also, as strictly monotonic
- for
- also
- using formula, we obtain:
- : cont. r.v. w/ pdf
- and is odd
- find:
- 👨🏫 exercise
- let be cont. r.v. w/ cdf
- assume : strictly increasing function
- define the r.b. by
- possible values of
- for
- PDF of : for
- thus,
- generating an exponential r.v.
- for
- then : value s.t.
- and : also follows
- thus
- let , find cdf, pdf. of
Joint Distribution Functions
-
Introduction
- often: we are interested in multiple r.v. at the same time
- e.g. a student's age, gender, major, year of study
- on particular day, number of vehicle accidents, deaths, and major injuries
- generalizing distribution function: for multiple r.v.s
- joint distribution function
- often: we are interested in multiple r.v. at the same time
-
Joint distribution function
- for r.v. in same , define joint distribution function of aas
- generalization of
- often abbreviated: joint d.f.
- remarks
- distribution of : obtained from joint d.f. by:
- then : marginal distribution function of (= cdf)
- properties
- 👨🏫 all derived from:
- for any
- for any
- for any
- for any
- 👨🏫 all derived from:
- using joint d.f. to compute two r.v.
-
- think about it in geometry!
- inclusion matters here!
-
- proof
- then
- thus:
- for r.v. in same , define joint distribution function of aas
-
Joint probability mass function
- joint pmf of :
- marginal pmf
- conditions to check for validity
- useful calculations
-
Example
-
suppose: balls randomly selected from urn
- w/ red, white, and blue balls respectively
- : rn. of white balls chosen
- pmf of is:
r\w 0 1 2 3 0 10/220 40/220 30/220 4/220 84/220 1 30/220 60/220 18/220 0 108/220 2 15/220 12/220 0 0 27/220 3 1/220 0 0 0 1/220 56/220 112/220 48/220 4/220 - last row & column: marginal pmf
-
suppose: 15% of family in community w/ no children
- 20% w/ 1
- 35% w/ 2
- 30% w/ 3
- each child: equally likely to be a boy or girl
- : no. of boys, : no. of girls
\ 0 1 2 3 0 0.1500 0.1000 0.0875 0.0375 0.3750 1 0.1000 0.1750 0.1125 0 0.3875 2 0.0875 0.1125 0 0 0.2000 3 0.0375 0 0 0 0.0375 0.3750 0.3875 0.2000 0.0375
-
Joint Continuous Random Variables
-
Joint and marginal pdf
- : jointly continuous r.v. if there exists joint pdf for every set
- marginal pdf: given by
- conditions to check: same as discrete
- some useful calculations
- for , take
- for where
- ⭐ for
- thus:
-
Examples
- joint pdf: given by
- =
- joint pdf: given by
MATH 2421: Lecture 16
Date: 2024-10-30 11:52:18
Reviewed:
Topic / Chapter:
summary
❓Questions
- ❓ let joint pdf of be circular: e.g.
- and let joint pdf be cylinder: extending in Z axis from the circle
- then, can we say ?
- 👨🏫 yes!
- ❓ what's so complex about continuous-discrete joint distribution?
- 👨🏫 its cdf is not well established
Notes
Joint Distribution Functions (cont.)
-
Examples
- joint density of : given by
- find: density of
- and
- joint density of : given by
Independent Random Variables
-
Independent r.v.
- two r.v. : independent if:
- for any
- i.e. value of not influencing probability of , vice versa
- else: they are dependent
- theorem: following statements are equivalent for jointly discrete / cont. r.v.
- r.v. are independent
- , we have:
- joint pmf = product of marginal pmf
- , we have:
- joint cdf = product of marginal cdf
- r.v. independent: iff s.t. for all
- () not necessarily being
- 👨🏫 joint pdf: factorizable
- same for cdf
- proof:
- for continuous case, independence factorizable
- for its pdf
- now:
- where :
- as ,
- where :
- for continuous case, independence factorizable
- two r.v. : independent if:
-
Examples
- given 3 balls randomly selected from urn
- containing 3 red, 4 white, 5 blue
- let : no. of red / white chosen
- are : independent?
- w/ independent trials, having common success probability
- : no. of success in first trials
- : no. of success in last trials
- doesn't influence , and vice versa
- : independent
- similarly
- and
- man an woman: decided to meet at a location
- each person: independently arrive at u.a.r. between 12 noon ro 1 pm
- find probability: first to arrive waiting longer than 10 minutes
- : time past 12 noon, in minutes, man arrives
- : time past 12 noon, in minutes, woman arrives
- if
- if
- if
- finding:
- thus ..?
- Buffon's needle problem: table ruled w/ equidistant parallel lines a apart
- needle: length
- randomly thrown on the table
- what is the probability that needle: intersect one of the lines?
- needle: length
- if ,
- are r.v. independent?
- solution 1
- find marginal pdf, and compare
- solution 2
- let
- for all
- and : not factorizable
- and thus: are not independent
- i.e. factorizable: we can define for all
- and : not factorizable
- basically: is factorizable if its region is shown as square, cube, etc.
- which edges are all parallel to the axis
- otherwise: impossible
- traffic accidents occur per day w/
- each accident: major & minor
- and it is a major accident w/
- let : denote no. of major & minor accidents, respectively
- , if , then
- find joint pmf of
- for
- are independent?
- yes, as it's factorizable by:
- within range
- within range
- yes, as it's factorizable by:
- can you identify: distribution of ?
- 👨🏫 exercise!
- each accident: major & minor
- given 3 balls randomly selected from urn
MATH 2421: Lecture 17
Date: 2024-11-04 11:44:02
Reviewed:
Topic / Chapter:
summary
❓Questions
- ❓ does implies pairwise independence, etc.?
- 👨🏫 Yes. As the condition is , it's fine
Notes
Independent Random Variables (cont.)
-
More than 2 r.v.
- joint pdf of multiple r.v. (e.g. ) can be described as:
- multiple cont. r.v. (e.g. ) are independent if, :
-
Examples
- suppose : independent standard normal dist.
- find: joint Pdf of
- from independence:
- let be independent & uniformly distributed over
- compute
- suppose : independent standard normal dist.
Sum of Independent random Variables
-
X, Y being continuous & independent
- theorem: on independence, for
- following:
- ⭐👨🏫 important
- : "convolution of "
- proof
- some of 2 important Gamma d.v.
- then
- proof
- ⭐👨🏫 sum of independent normal r.v.
- for where
- use linearity
- d
- theorem: on independence, for
-
X, Y being discrete & independent
- pmf of , each being discrete r.v.:
- similarly, for continuous r.v.:
-
Exercises
- X+t\leq (0,2)2-xd_{X+Y}(x,) w/ triangular dist."
- : dimctop smooth triangular
- basketball team: plays a 44-game season
- 26 games: against class A; 18: against class B
- chance of against class A:
- chance of against class B:
- result of different games: independent
- : no. of wins against class
- compute or (👨🏫 either works)
- 👨🏫 use normal approximate
- sum of independent normal: normal dist.
- compute
- then
- sum of 2 indep. binomial r.v.
- , indep.
- find pmf of
- s
- X+t\leq (0,2)2-xd_{X+Y}(x,) w/ triangular dist."
Lecture 18
MATH 2421: Lecture 19
Date: 2024-11-11 11:54:21
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Joint PDF of Functions of RV
-
Generalization to multiple variables
- 👨🏫 for exams: you are expected to do max.
- Jacobian determinant expands, to
-
Example
- let : jointly continuous r.v. w/ pdf
- let
- find joint density function of in terms of
- d
- suppose : independent standard normal variable
- show: are independent normal variables
- let
- and
- as they are independent:
- by previous example: joint pdf of is
- as con
- let be independent standard normal
- then
- pdf of
- domain:
- thus, pdf of :
- for joint pdf is factorization, are independent
- : uniform distribution
- 👨🏫 rotation ignorance property of normal vectors
- : uniform distribution
- : Rayleigh distribution
- if : independent Gamma r.v. w/ parameters
- compute joint density of
- Finally, joint pdf of :
- try harder later
- let : jointly continuous r.v. w/ pdf
Jointly Distributed R.V w/ n>2
-
Jointly distributed r.v.
- marginal distribution, namely:
- similar for density function
Expectation of Sum of Random Variables
-
Expectation of sum of random variables
- theorem:
- proof:
- if : jointly discrete w/ joint pmf
- if : jointly continuous w/ joint pdf
- remarks
- if whenever , then
- Monotone property, if , then
- important special case
- mean of sum: sum of means
-
- leads to: linearity of expectation regardless of independency
- to compute the sum: marginal pdf / pmf is enough
- d
-
Example
- accident: at point w/ uniformed distributed on a road of length
- ambulance: at location , uniformly distributed on the same road
- find: expected distance between the ambulance and point of the accident
- joint pdf: multiplication!
- sample mean: let : independent & identically distributed r.v.
- w/ distribution function and expected value
- such sequence of r.v.: constitute a sample from distribution
- sample mean : defined as
- Boole's inequality (skipped)
- mean of hypergeometric
- balls: selected from balls of which are white
- find expected no. of white balls selected
- : no. of white balls selected
- use indicator random variable
- balls: selected from balls of which are white
- accident: at point w/ uniformed distributed on a road of length
Math 2421: Lecture 20
Date: 2024-11-13 12:01:10
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Expectation of Sum of Random Variables
-
Example
- people: throw their hats to center of a room
- hats: mixed up, find expected no. of people getting back their own hats
- suppose: different types of coupons exists
- and each time: obtaining a coupon is equally likely to be any of types
- find: expected no. of different types with run
- denote answer by
- for
- : 1 if -th type is contained in the company
-
- denote answer by
- find expected no. of coupons needed before completing at lease one set of each type
- let : no. of coupons needed to get a complete set
- : no. of coupons you need in order to get a first new type
- : no. of coupons you need in order to get a second a new type (after )
- : no. of coupons to get a new type after collecting types
- where success probability
- thus:
- people: throw their hats to center of a room
Covariance, Variance of Sums, and Correlations
-
Covariance
- covariance of jointly distributed r.v. :
- measures: how vary together
- common formula
- if, for larger value of : corresponds to larger values of
- then
- else:
- remark: if , : correlated
- else: : uncorrelated
- correlation: does not imply causation
- theorem:
- similar to
- proof
- theorem: if independent, then for any , we have
- theorem: if independent: then
- 👨🏫 however: doesn't mean that are independent
- proof: set some s.t. , and let dependent on
- and let always
- then
- theorem:
- proof:
- w/ independent
- under independence:
- proof:
- covariance of jointly distributed r.v. :
-
Properties of covariance
- 👨🏫 no independence assumed
- d
-
Covariance
-
Example
- sample variance
- is called deviation
- sample variance:
- find
- w/ independence:
- find
- thus, sample variance w/ is a good estimator
- sample variance
MATH 2421: Lecture 21
Date: 2024-11-18 11:59:35
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Covariance, Variance of sums, and Correleations (cont.)
-
Covariance
- correlation (coefficient) of r.v. : defined by defined by:
- thus:
- proof
- remarks
- d
- iff w/
- tjere
- s
- if w/
- d
- independence of implies
- but the opposite: doesn't get support
- d
-
Example
- variance of binomial
- : given by
- : whether -th trial is success / not
- example
- , w/ fair probability
- if , if
- , and as ,
- variance of binomial
Conditional expectation
-
Conditional expectation
- w/ : jointly distributed discrete r.v.
- w/
-
- a valid PMF!
- w/ : jointly distributed continuous r.v.
- w/
- w/ a valid PDF!
- important formula
- s
- thus: conditional expectation of sum = sum of conditional expectation
- s
- furthermore, consider as function of ,
- e.g. , then
- theorem:
- i.e. nesting property of expectation
- and
- d
- w/ : jointly distributed discrete r.v.
-
Example
- for :
- d
- f
MATH 2421: Lecture 22
Date: 2024-11-20 11:27:40
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Conditional Expectation (cont.)
-
Conditional expectation
- we may also use this approach to compute probabilities
- s.t. w/ being an event
- then
- then
- we obtain:
- we obtain:
- e.
- s.t. w/ being an event
- d
- we may also use this approach to compute probabilities
-
Example
- miner: trapped in a mine w/ 3 doors
- first door: to a safety place after 3 hours
- second door: back to same place after 5 hours
- third door: back to same place after 7 hours
- choosing each door: equally likely
- and previous choice is forgotten
- find: expected length of time, until the miner reach the safety
- let : length of time until reaching the safety
- : door number he chooses
- expectation of a random sum
- suppose: are iid w/ common mean
- let non-negative, integer valued r.v. independent of
- our interest: mean of
- where : taken to be zero when
- solution
- suppose: no. of people getting department store on a day: r.v. w/
- amounts of money spent by individual customers: indep. r.v. w/ common mean
- suppose amount of money spent by a customer: independent of total no. customers entering
- what is: expected amount of money spent on a given day?
- : independent w/ pdf . Compute
- conditioning on the value of
- let be u.r.v. and define conditional density is
- miner: trapped in a mine w/ 3 doors
Conditional Variance
-
Conditional variance
- pre-req
- conditional variance of given
- notably:
- proof
- 👨🏫 not often used, and its application is not expected
-
Example
- 👨🎓 (very complicated computation)
Moment Generating Function
-
Moment generating function
- moment generating function of r.v. , is defined as:
- called as MFG as:
- it generates moments of r.v. for
-
- where
- proof: by Taylor series expansion
- and
- equating coefficient of , we get
- 👨🏫 not all r.v. has a mgf
- e.g. for cauchy distribution, does not exist for , and has no mgf
- 👨🏫 for advanced topics, people use complex numbers and find ways
- e.g. for cauchy distribution, does not exist for , and has no mgf
- and
- theorem: multiplicative property
- if independent:
- proof
- theorem: uniqueness property
- let be r.v. w/ their MGF
- suppose there exists an s.t.
- then have the same distribution (i.e. or )
MATH 2421: Lecture 23
Date: 2024-11-25 12:00:07
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Moment Generating Function (cont.)
-
Moment generating function
-
Examples
- when
- when
- , being independent and
-
- 👨🏫 exercise!
- when
- suppose
- derive the 4th moment by computing 4th derivative
- 👨🏫 tedious!
- when
- when for
- as otherwise, - somewhat impossible:
- as = frequency can't be negative!
- as otherwise, - somewhat impossible:
- when
- , where
- compute first
- suppose , find
- given: Poisson distribution
- sum of independent Binomial r.v. w/ the same success probability: binomial
- , , being independent
- thus
- similar for Poisson r.v.
- sum of independent normal r.v. is normal
- find all moments of exponential dist. of parameter
- thus:
- chi-squared r.v. w/ degrees of freedom:
- given as:
- : independent std. normal r.v.
- then :
- given as:
- when for
Joint Moment Generating Functions
-
Joint MGFs
- for multiple variables:
- thus: for joint distribution of
- exists joint cdf, pmf/pdf, and joint mgf
- joint mgf:
- exists joint cdf, pmf/pdf, and joint mgf
- individual mgf: can be obtained from joint mgf (like marginal)
- 👨🏫 not required for the final exam
- for multiple variables:
-
Multiplication rule
-
- iff each independent
- proof: too advanced for this course
- but some generalization of the original multiplication rule
-
-
Example
- let be independent normal r.v. w/
- as we know that are independent, we get:
- if we considered the original preceding as a sum of normal r.v. with
- and indep. normal r.v. w/
- joint MGF: uniquely determines the joint distribution
- thus: and are independent normal r.v.
- if we considered the original preceding as a sum of normal r.v. with
- as we know that are independent, we get:
- let be independent normal r.v. w/
Limit Theorem
-
Introduction
- 2 important concepts: laws of large numbers & central limit theorem
- LLN: concerned w/ stating conditions under the average of a seq. of r.v. converges to expected average
- CLT: concerned w/ determining conditions: where sum of large number of r.v. has probability distribution approximately normal
-
Chebyshev's inequality and weak law of large numbers
- inequalities below: for estimating tail probabilities w/ minimal information on r.v.
- e.g. its mean / variance
- Markov's inequality: for non-negative r.v. and for :
- proof: (~= first moment)
- Chebyshev's inequality: for r.v. w/ finite mean , variance , then for :
- proof: (~= first moment)
- Markov's & Chebyshev's: deriving bounds on probabilities with very few information
- mean / mean & variance
- if the actual distribution is not known: it's a decent measure!
- inequalities below: for estimating tail probabilities w/ minimal information on r.v.
-
Example
- no. of items produced in factory: a r.v. w/ mean 50
- what is: probability that production exceed 75?
- if variance of production is 25, what is the probability of production being within ?
- what is: probability that production exceed 75?
- no. of items produced in factory: a r.v. w/ mean 50
Tutorial 7
Tutorial 8
Tutorial 9
Tutorial 10
MATH 2421: Tutorial 11
Date: 2024-11-26 18:03:39
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Tutorial
-
Tutorial
- conditional expectation & variance
- conditional expectation
- law of total expectation
- 👨🏫 idea: separating randomness
- then
- 👨🏫 idea: separating randomness
- conditional variance
- moment generating function
- if independent:
- uniqueness: MGF determines distribution uniquely
- i.e. if two r.v. have same MGF: then same distribution
- law of large number (LLN)
- if : i.i.d. r.v. w/
- i.e. convergence in probability
- a.s.: almost sure
- convergence in probability
- 👨🏫 probability of not converging = 0
- 👨🏫 for stronger result, a stronger assumption is needed
- can be computed without knowing the distribution of individual r.v.
- must exist, though
- if : i.i.d. r.v. w/
- central limit theorem (CLT)
- if : i.i.d. r.v. w/
- i.e. convergence in distribution
- strength of convergence: almost sure > in probability > in distribution
- one on the left: implies one on the right
- conditional expectation & variance
-
Examples
- skipped
- solution
- let
- show: w/ distribution
- for all
- idea: law of total probability, solving one by one
- explanation: set
- integrate both sides to show: one converges to
- consider: a very simple case for intuition
- :
- let
- Poisson w/
- show:
- Poisson's MGF:
MATH 2421: Lecture 24
Date: 2024-11-27 11:59:13
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Limit Theorem
-
Laws of large numbers
- weak law of large numbers: for iid r.v. w/ common mean
- then, for any
- proof: under additional assumption
- assumption: r.v. w/ finite variance , it's given that
- from Chebyshev's inequality:
- weak law of large numbers: for iid r.v. w/ common mean
-
Applications
- casino games
- in long run / repetition: casino's profit = expected value of gambling
- e.g. 1/381 cost per trial
- insurance
- polling: estimating opinions of a large population
- stock market: average return converge to the historical average
- casino games
-
Central limit theorem
- 👨🏫 one of the most remarkable result
- stating: sum of large no. of indep. r.v.: follows approximately normal dist.
- not only a simple method for approximation of sum
- but also explaining remarkable fact for empirical freq.
- of natural population exhibiting bell-shape curves
- stating: sum of large no. of indep. r.v.: follows approximately normal dist.
- central limit theorem: w/ iid r.v. w/
- distribution of:
- tends to standard normal as :
- LHS: CDF, RHS:
- thus:
- examples
- human heigh, IS, test scores, blood pressure, etc.
- remarks: while the theorem itself is also important
- discoveries made on the way to the theorem were also significant
- : can be approximated by normal distribution as:
- it's sum of iid Bernoulli r.v.
- 👨🏫 one of the most remarkable result
-
Examples
- w/ independent r.v.
- each w/ uniform distribution over
- calculate: approximation to
- no. of students enrolling in a psychology class: Poisson r.v. w/
- prof. in charge: will teach the course in 2 sessions, if 120 or more enrolls
- what's the probability of teaching 2 sessions?
-
- exact answer, but we might better approximate
- w/ iid and
- normal approximation: w/ of independent uniformly distributed r.v. over
- estimate / upper bound:
- use Markov's inequality to obtain an upper bound
- use Chebyshev's inequality to obtain an upper bound
- use Central Limit Theorem to approximate
- although Markov and Chebyshev's upper bound is not very tight, it's widely used
- w/ independent r.v.
-
Strong law of large numbers
- best-known result in probability theory
- strong law of large numbers
- w/ a seq. of iid r.v.
- each w/ finite mean
- then, w/ probability 1:
- alternatively:
- w/ a seq. of iid r.v.
-
Example
- suppose: seq. of independent trials of some experiment
- let : fixed event of experiment
- let : chance of occurring on any particular trial
- let:
- w/ Strong law of large numbers, w/
- : corresponds to proportion of time occurs in first trials
- thus: interpret the result as:
- w/ , limiting proportion of times that occurs:
- let : fixed event of experiment
- suppose: seq. of independent trials of some experiment
Final exam remarks
-
Remarks
- Dec. 9th, 12:30 - 2:30 (2 hr)
- TST Sports Ctr Arena (Seafront)
- covers: Ch. 5-8 (from continuous r.v.)
- yet, Ch. 1-4 might be implicitly included
- e.g. famous discrete distributions from Ch. 4
- Be, Bin, Geom, Poisson
- e.g. famous discrete distributions from Ch. 4
- yet, Ch. 1-4 might be implicitly included
- conditional variance: only concept is required
- join distribution of r.v. / joint MFG is not covered in final
- 👨🏫 Beta, Gamma, Cauchy, etc. won't be major component
- exam format
- each question: 20 pt,
- w/ possible subproblems
- 6 questions
- 1 A4 size 2 sided cheat sheet allowed
- normal table: provided
- same as one in past papers
- calculator: anything without internet access
- Dec. 9th, 12:30 - 2:30 (2 hr)
-
Some policies
- seating plan to be released
- bring your SID, calculator, cheat sheet, etc.
Ch. 7 Revision
-
Example
- mean of hypergeometric:
- balls chosen randomly from an urn w/ balls, where are white
- find: expected number of white balls selected
- find: variance of white balls selected
- for
- mean of hypergeometric: