Cornell Format

Date:

Reviewed:

Topic / Chapter:

summary

❓Questions

Notes

Topic 1

Date: 2024년 7월 2일

Reviewed:

Topic / Chapter:

❓Questions

Notes

Programming ZKP
- Programming ZKP
  - converting idea into work
    - programmer: idea → high-level language
    - compiler: high-level language → R1CS
      - focus of today
    - setup: R1CS → param
    - prove: param → ZKP
    - verify: param * ZKP → {0,1}
- ZKP basics
  - ZKPs for a predicate $ϕ$
    - prover knows $ϕ, x, w$
    - verifier: knows $ϕ, x$
    - proof $π$ : shows $ϕ (x, w)$ holds
      - but not reveals $w$
    - what can be $ϕ$ ?
  - $ϕ$ in theory: any NP problem
    - e.g. $w$ : factorization of $x$
    - e.g. $w$ secret key for public key $x$
    - etc.
  - $ϕ$ in practice: arithmetic circuit over input $x, w$
- Arithmetic circuits (ACs)
  - domain: prime field
    - $p$ : a large (~255 bit) prime
    - $Z_{p}$ : integers $mod p$
      - (modular) operations: $+, \times, =$
  - approach 1: as a systems of field equations
    - e.g. $w_{0} \times w_{0} \times w_{0} = x$
      - $w_{1} \times w_{1} = x$
  - approach 2: as circuits
    - directed, acyclic graph
    - nodes: inputs, gates, constants
    - edges: wires / connections
    - (for the same eg)
```
graph LR
  w_0[w_0] --> OPtimes_0([x])
  w_0[w_0] --> OPtimes_0([x])
  w_0[w_0] --> OPtimes_0([x])
  OPtimes_0([x]) --> OPeq_0([=])
  w_1[w_1] --> OPtimes_1([x])
  w_1[w_1] --> OPtimes_1([x])
  OPtimes_1([x]) --> OPeq_1([=])
  
  x[x] --> OPeq_0([=])
  x[x] --> OPeq_1([=])
  
```
- Approach 3: Rank 1 Constraint Systems (R1CS)
  - R1CS: format for ZKP ACs
  - definition (linear combination)
    - $x$ : field elements $x_{1}, \dots, x_{l}$
    - $w$ : $w_{1}, \dots, w_{m - l - 1}$
    - $ϕ$ : $n$ equations of form
      - $α \times β = γ$
      - $α, β, γ$ : affine combination of variables / constants
    - examples
      - $w_{2} \times (w_{3} - w_{2} - 1) = x_{1}$
        
        $α = w_{2}$
        
        $β = w_{3} - w_{2} - 1$
        
        $γ = x_{1}$
      - $w_{2} \times w_{2} = w_{2}$
      - ❌ $w_{2} \times w_{2} \times w_{2} = x_{1}$
        
        $w_{2} \times w_{2} = w_{4}$
        
        $w_{4} \times w_{2} = x_{1}$
  - matrix definition
    - $x$ : vector of $l$ field elements
    - $w$ : vector of $m - l - 1$ field elements
    - $ϕ$ : matrices $A, B, C \in Z_{p}^{n \times m}$
      - $z = (1∣∣ x ∣∣ w) \in Z_{p}^{m}$
      - holds when $A z \circ B z = C z$
        
        i.e. element-wise product
    - each rows of $A, B, C$ : coefficients for each R1CS
      - width: 1 more than no. of variables to include constants
- Writing an AC as R1CS
  - example illustrated
```
graph LR
  w_0[w_0] --> OPtimes_0([x])
  w_1[w_1] --> OPtimes_0([x])
  w_1[w_1] --> OPtimes_1([x])
  OPtimes_0([x]) --w_2--> OPplus_0([+])
  OPplus_0([+]) --w_3--> OPeq_0([=])
  
  x_0[x_0] --> OPplus_0([+])
  x_0[x_0] --> OPtimes_1([x])
  OPtimes_1([x]) --w_4--> OPeq_0([=])

  
```
  - procedure
    1. write intermediate $w$ s
    2. write equations
      1. $w_{0} \times w_{1} = w_{2}$
      2. $w_{3} = w_{2} + x_{0}$
        
        $β = 1$ ; $γ = w_{2} + x_{0}$
      3. $w_{1} \times x_{0} = w_{4}$
      4. $w_{3} = w_{4}$
  - now: how to convert high-level $ϕ$ to R1CS?
    - R1CS: like assembly
    - conversion from $ϕ \to$ R1CS: w/ libraries, compilers, etc.
  - most zk products: built similarly
    - high-level code → compiler / library → R1CS → ZK proof system
  - example: Zcash
    - $ϕ$ : definition of “spending money anonymously”
    - circuit: involves
      - Merkle tree
      - Pedersen hash
      - signatures
      - spend logic
      - etc.
    - written in Bellman library ⇒ R1CS
      - three tool types:
        
        HDL
        
        Library
        
        PL + compiler
    - R1CS: fed into Groth16 (runs on user computer)
Using an HDL
- Circom basics
  - Circom: Hardware Description Language
    - ≠ programming languages
  PL HDL
  
  Objects variables
  
  operations
  
  programs / func wires
  
  gates
  
  circuit / sub-circ
  
  Actions mutate variables
  
  call functions connect wires
  
  create sub-circuits
  - HDLs for Digital Circuits
    - Verilog (dominate)
    - System Verilog
    - VHDL
    - Chisel
  - Circom: HDL for R1CS
    - wires: R1CS variables
    - gates: R1CS constraints
    - circuit: does 2 things
      - sets variable values
      - create R1CS constraints
- Circom: base language
  - example code
```
template Multiply() {
	signal input x;
	signal input y;
	signal output z;
	
	z <-- x * y;
	z === x * y;
	
}

component main {public [x]} =
	Multiply();
```
  - a template: is a (sub) circuit
  - a signal is a wire
    - input or output as property
  - <--: sets signal values
  - ===: creates constraints
    - must be rank-1
    - one side: linear; another: quadratic
  - <==: does both (shorthand)
  - specify that this template is the main
    - also which signals are public and which are not
    - input: implicitly private
    - output: implicitly public
- Circom: metaprogramming language
  - example
```
template RepeatedSquaring(n) {
	signal input x;
	signal output y;
	
	signal xs[n+1];
	xs[0] <== x;
	for (var i = 0; i < n; i++) {
		xs[i+1] <== xs[i] * xs[i];
	}
	y <== xs[n];
}

component main {public [x]} = 
	RepeatedSquaring(1000);
```
  - template arguments (fixed at compile time)
    - e.g. length for signal arrays
  - variables
    - mutable
    - not signals
    - evaluated at compile-time
  - loops
  - if statements
  - array accesses
- Circom: witness computation & sub-circuits
  - guaranteeing non-zero
```
template NonZero() {
	signal input in;
	signal inverse;
	inverse <-- 1 / in; // not R1CS
	1 === in * signal; // is R1CS
}

template Main() {
	signal input a; signal input b;
	component nz = NonZero();
	nz.in <== a; // quits if a == 0
	0 === a * b; // asking: is B zero?
}
```
  - idea: to ask whether there exists multiplicative inverse
  - <--: more general than ===
  - components hold sub-circuits
    - access inputs / outputs w/ dot-notation
Circom Tutorial
- Implementing sudoku
  - $x$ : puzzle
  - $w$ : solution
  - $ϕ$ : goal & rules
    - for simplification: forcing only no-duplicates-in-a-row rule
  - roadmap
    - implement notEqual (i.e. difference ≠ 0)
    - implement Distinct(n) from not Equal
    - implement Bits4 or in % 16 === in
    - implement OneToNice by computing
      - Bits4 on in-1
      - Bits4 on in+6
    - implement Sudoku by
      - check whether all numbers are in range
      - check whether solution matches the puzzle
      - check whether all numbers in the same row are distinct

	PL	HDL
Objects	variables
operations
programs / func	wires
gates
circuit / sub-circ
Actions	mutate variables
call functions	connect wires
create sub-circuits

Using a Library

Library for R1CS
- Circom key features
  - direct control over constraints
  - custom language
    - can be good / bad
- alternative: library in a host language
  - Rust, OCaml, C++, Go…
- key type: constraint system
  - maintains state about R1CS constraints & variable
    - i.e. value for variables & $A, B, C$
  - key operations
    - create variable
    - create linear combinations of variables
    - add constraint
Pseudo-rust example
- variable creation
  - cs.add_var(p, v) -> id
  - cs: constraint system
  - p: visibility of variable
  - v: assigned value
  - id: variable handle
- linear combination creation
  - cs.zero(): returns the empty LC
  - lc.add(c, id) -> lc'
  - id: variable (handle)
  - c: coefficient
  - lc' := lc + c * id
- adding constraints
  - cs.constrain(lc_a, lc_b, lc_c)
  - adds constraint lc_a * lc_b = lc_c

Example code: Boolean AND

#![allow(unused)]
fn main() {
fn and(cs: ConstraintSystem, a: Var, b: Var) -> Var {
	let result = cs.new_witness_var(|| a.value() & b.value());
	self.cs.enforce_constrant(
		lc!() + a,
		lc!() + b,
		lc!() + result,
	);
	result
}
}

Leverage language abstractions

e.g. using structs, operator overloading, etc.

#![allow(unused)]
fn main() {
struct Boolean {var: Var};

// i.e. & overloading
impl BitAnd for Boolean {
	fn and(self: Boolean, other: Boolean) -> Boolean {
		// same as before
		Boolean {var: result}
	}
}
}

example usage

#![allow(unused)]
fn main() {
let a = Boolean::new_witness(|| true);
let b = Boolean::new_witness(|| false);
(a & b).enforce_equal(Boolean::FALSE);
}

many different gadget libraries
- libsnark: gadgetlib (C++)
- arkworks: r1cs-srd + crypto-primitives (Rust)
- Snarky (Ocaml)
- Gnark (Go)

Witness computation

can perform arbitrary computations to generate witnesses
- more freedom as it’s general-purposed language!

#![allow(unused)]
fn main() {
let a = Boolean::new_witness(|| (4 == 5) & (x < y));
let b = Boolean::new_witness(|| false);
(a & b).enforce_equal(Boolean::FALSE);
}

closure / lambda ||: executed only during proving

Arkworks Tutorial (Rust)

Using a Compiler

HDL & circuit libraries comparison
- differences:
  - host language vs. custom language
- similarities
  - explicit wire creation
  - explicit constraint creation
  - 👨‍🏫is it necessary?
    - No! by creating a new language, we can avoid it!

ZoKrates syntax

#![allow(unused)]
fn main() {
type F = field;

def main(public F x, private F[2] ys) {
	field y0 = y[0];
	field y1 = y[1];
	assert(x = y0 * y1);
}
}

struct syntax for custom types
variables: contain values during execution / proving
can annotate privacy
“assert” creates constraints
main function exists
other language features
- integer generics
- arrays
- variables
  - mutable
- fixed-length loops
- if expressions
- array accesses

feature example

#![allow(unused)]
fn main() {
def repeated_squaring<N>(field x) -> field {
	field[N] mut xs;
	xs[0] = x;
	for u32 i in 0..N {
		xs[i + 1] = xs[i] * xs[i];
	}
	return xs[N];
}

def main (public field x) -> field {
	repeated_squaring::<1000>(x)
}
}

short: no way to compute witnesses

all witnesses: must be provided as input

#![allow(unused)]
fn main() {
def main(private field a, public field b) {
	assert(a * b == 1)
}
}

ZoKrates Tutorial (~= Rust)
- Compilation
  - compile: zokrates compile -i root.zok
  - setup: zokrates setup
  - witness computation: zokrates compute-witness -a 1 0 0 2 1 2 1 2
    - or: [[1,0], [0,2]] and [[1,2],[1,2]]
  - proof generation: zokrates generate-proof
  - verification: zokrates verify

Overview of Prominent ZKP Toolchains

A quick tour

toolchain type
- HDL: language for circuit synthesis description
- library: library for describing circuit synthesis
- PL + compiler: a language, compiled to a circuit
organized view

language type standalone?

no yes

circuit library (Arkworks) HDL (Circom)

program PR (ZoKrates)

language type	standalone?
	no	yes
circuit	library (Arkworks)	HDL (Circom)
program		PR (ZoKrates)

pros and cons

type	Circom	Arkworks	ZoKrates
pros	clear constraints
elegant syntax	clear constraints
as expressive as Rust	easiest to learn
elegant syntax
cons	hard to learn
limited abstraction (no types, etc.)	need to know Rust
few optimizations	limited witness computation

other toolchains

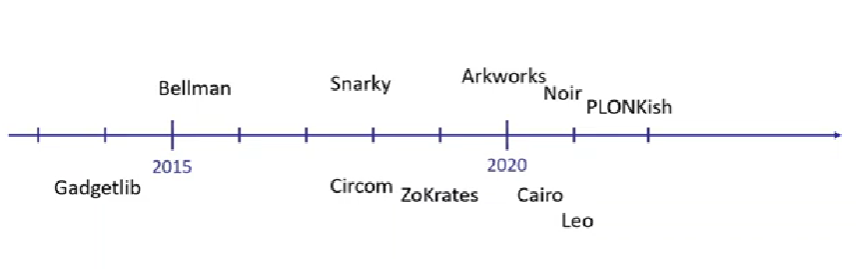
HDL Library PL + Compiler

Circom Arkworks (Rust) ZoKrates

Gadgetlib (C++) Noir

Bellman (Rust) Leo

Snarky (OCaml) Cairo

PLONKish (Rust)
timeline
shared compiler infrastructure?
- source: (many PLs)
- target: R1CS, Plonk, AIR
- common techniques
  - Boolean
  - fixed-width ints
  - variables
  - mutation
  - structures
  - control flow
  - optimization
  - arrays
- 👨‍🏫can we build a library to create a PL for ZKP with this common ground?
  - attempt: CirC

HDL	Library	PL + Compiler
Circom	Arkworks (Rust)	ZoKrates
	Gadgetlib (C++)	Noir
	Bellman (Rust)	Leo
	Snarky (OCaml)	Cairo
	PLONKish (Rust)

Zero Knowledge Proof MOOC