Date:
Reviewed:
Topic / Chapter: SNARKs via Interactive Proofs
❓Questions
Notes
- Interactive Proofs
- Motivation
- computation-limited verifier
- wants data analysis
- verifier: holds data summary
- queries to cloud provider w/ data
- or: “challenges”
- cloud provider: provides answer
- queries to cloud provider w/ data
- interactive proofs (formally)
- solves problem, tells the answer
- then conversation goes
- ’s goal: convince the answer is correct
- requirements
- completeness: an honest can convince
- (statistical) soundness: will catch ’s lie w.h.p.
- if soundness holds only against “eff” provers: then it is argument not proof
- solves problem, tells the answer
- computation-limited verifier
- Interactive proofs vs. arguments
- soundness vs. knowledge soundness
- soundness: accepts → s.t.
- knowledge soundness: accepts → “knows” s.t.
- 👨🏫stronger!
- standard soundness: meaningful even when knowledge soundness isn’t
- as there is no “natural witness”
- e.g. claims that output of ’s program on is 42
- reverse: prover claims he knows secret key for a certain BTC wallet
- or: preimage of hash that gives 0
- many “witnesses” exist
- public verifiability
- only convincing the party that is choosing random challenges
- others: can’t trust the proposed verifier
- if interactive: each run only convinces one party
- for public coin protocols: Fiat-Shamir is used
- to make it non-interactive
- only convincing the party that is choosing random challenges
- soundness vs. knowledge soundness
- Motivation
- SNARKs from Interactive Proofs
- SNARK example
- procedure
- : commits cryptographically to
- reveals “just enough” info on commitment to allow to run checks
- render non-interactive via Fiat-Shamir
- procedure
- SNARK example
- Review of Functional Commitments
- Functional commitments
- different types
- polynomial commitments
- to univariate
- multilinear commitments
- to multilinear
- vector commitments (e.g. Merkle trees)
- to
- open cells:
- polynomial commitments
- different types
- Merkle trees: the commitment
- uses: C.R. hash function
- opening proof size:
- example: univariate
-
- …
- to prove value , must provide
- , , ,
-
- notation
- Merkle-commits to all evaluations of
- upon request of , reveals all associated leaf along w/ opening info
- two problems
- no. of leaves:
- takes at least to compute commitment
- want time proportional to degree bound
- does not know has at most degree
- no. of leaves:
- Functional commitments
- Interactive Proof Design: Technical Preliminaries
- SZDL lemma
- FACT: let be univariate polynomials of degree at most
- then
- has at most zeros
- SZDL lemma: multivariate generalization
- let be -variate polynomials of total degree at most
- then
- using multivariate to lower the degree and make computation quicker
- FACT: let be univariate polynomials of degree at most
- Low-degree and multilinear extensions
- extension: given , a -variate polynomial over : extend
- if
- multilinear extensions: any function has unique multilinear extension (MLE)
- multilinear: polynomial has degree at most 1 in each var
- e.g. , but not in
- extension: given , a -variate polynomial over : extend
- Example
-
let s.t.
1 2 8 10 -
(multilinear extension)
-
- actually: quite similar to SoP approach!
1 2 3 4 5 6 8 10 12 14 16 18 15 18 21 24 27 30 22 26 30 34 38 52 29 34 39 44 49 56 - True as:
-
-
non-multilinear extension
1 2 3 4 5 6 8 10 12 14 16 18 13 16 19 22 25 28 16 20 24 28 32 36 17 22 27 32 37 42 - True as:
-
- Evaluating multilinear extensions quickly
- fact: given as input evaluations of a function
- -time algo to evaluate
- i.e. by listing all its values with manually
- sketch: using Lagrange interpolation
- define
- i.e. multilinear Lagrange basis polynomial corresponding to
- or: PoS, but from analog values of
- ( being digital)
- fact:
- , can be computed w/ field operations
- yields an -time also
- can reduce to time via DP
- fact: given as input evaluations of a function
- SZDL lemma
- Sum-Check Protocol
- Sum-check protocol
-
[LFKN90]
-
input: given oracle access to a -variate polynomial over field
- i.e. access to where
-
goal: compute the quantity
- idea: outsource the computation to prover so that it takes time instead of
-
👟Start: sends claimed answer
- protocol checks that:
-
👟Round 1: sends univariate polynomial claimed to equal
- i.e. output if prover was honest
-
checks that
- or:
-
if check passes: safe to believe that is the correct answer
- if believes
- i.e. check where
- can compute directly from ’s first message, not though
-
👟Round 2: ( sends and) recursively check that
- i.e. that
-
👟Round : ( sends and) check that
- : checks that
- by picking
-
general idea: checking only on first occurrence, trusting it there after
-
- Sum-check protocol
- Analysis of Sum-Check Protocol
- Completeness
- holds by design
- if sends the prescribed messages: all tests will pass
- Soundness
- if some other message was sent: rejects w/ probability of at least
- e.g. , ,
- then soundness error
- proof: by induction on no. of var
- base case: ; sends claims to equal
- picks at random, checks that
- if , then
- inductive case
- recall: ’s first message claimed to equal
- picks at random, (recursively) checks that
- if , then
- if , is left to prove a false claim in rec. call
- applies sum-check to variate
- by induction: convinces w/ probability at most
- base case: ; sends claims to equal
- summary: if , accepts at most
- Cost of the protocol
- total communication: field elements
- sends messages, each at univariate degree
- sends messages, each w/ 1 field element
- ’s runtime:
- ’s runtime (at most)
- total communication: field elements
- Completeness
- Sum-Check Protocol Application
- Counting triangles
- input:
- representing adjacency matrix of a graph
- desired output:
- fastest known algorithm: runs in matrix-multiplication time
- i.e. ~= (super linear time)
- IP: let verifier run in time (minimum possible)
- input:
- Protocol
-
protocol: view
-
: multilinear extension of
-
define polynomial
-
apply the sum-check protocol to compute
-
- Costs
- total communication:
- runtime:
- runtime:
- runtime: dominated by evaluating
- Counting triangles
- SNARK for Circuit-Satisfiability
-
SNARK for circuit-satisfiability
- : agreed on circuit over size and output
- claims to know s.t.
- let be empty for simplicity
- transcript for : assignment of a value to every gate
- is correct if it assigns gate values upon evaluating on a valid
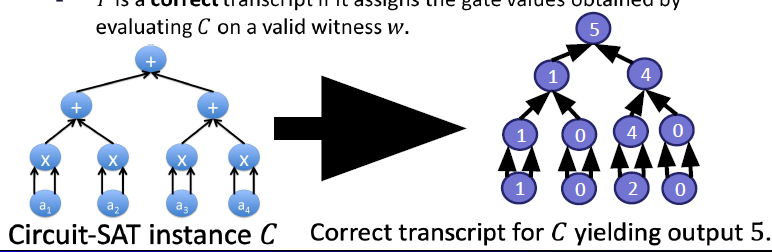
- : agreed on circuit over size and output
-
Transcript as a function
- with domain
- assign each gate in a ()-bit label and view as a function
- mapping gate labels to
- and final output: always (last gate to be computed)
-
- Polynomial IOP Underlying the SNARK
-
Polynomial IOP
- ’s first message is a ()-variate polynomial claimed to extend a correct transcript
- i.e.
- : needs to check this, but only able to learn few evaluation of (not )
- ’s first message is a ()-variate polynomial claimed to extend a correct transcript
-
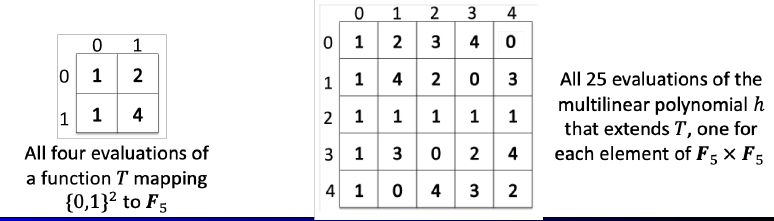
Intuition on
- : distance-amplified encoding of
- domain of :
- but domain of : much larger ()
- 👨🏫small difference in → vast difference (almost all) in extension
- due to distance-amplifying nature
- by Schwartz-Zippel
-
Two-step plan
- step 1: given any ()-variate polynomial , identify a related ()-variate polynomial s.t.
- extends a correct transcript ↔
- or: “vanishing” over Boolean hypercube
- i.e. if is not a correct transcript:
- ~= abstraction of messy structure?
- also: to evaluate at any input: evaluating at 3 inputs are enough
- extends a correct transcript ↔
- step 2: design an IP to check
- in which only needs to evaluate at one point
- step 1: given any ()-variate polynomial , identify a related ()-variate polynomial s.t.
-
Sketch
- step 1 sketch: define via:
- : gets 3 Boolean vectors in input
- returns 1 iff is addition gate and 2 neighbors are
- else 0
- : gets 3 Boolean vectors in input
- returns 1 iff is multiplication gate and 2 neighbors are
- else 0
- properties
-
- if is label computing sum of
-
- if is label computing multiplication of
- otherwise
- computation: can be outsourced to as it only depends on wiring structure, and thus being able to be committed
-
- step 2: how to check
- by evaluating at a single point?
- if were a univariate polynomial
- and we need to check that vanishes over some set , not
- fact: ↔ is divisible by
- : vanishing polynomial for
- 🧑🎓kind of trivial
- polynomial IOP
- sends a polynomial s.t.
- checks this by picking a random and checking
- step 1 sketch: define via:
-
Actual protocol
- above: not works as is not univariate
- computing (finding ) is expensive
- in final SNARK: it would be applying poly-commit to additional polynomials
- Marlin, PlonK, Groth16 does this, though
- solution: use the sum-check protocol
- handles multivariate polynomials
- doesn’t require to send additional large polynomials
-
- Polynomial IOP for Circuit-Satisfiability
- Recall sum-check
- goal: compute the quantity (all sum)
- proof length: roughly total degree of
- no. of round:
- time: ~= time to evaluate
- not necessarily revealing info on as long as it knows for random
- General idea
- (works over integers, for ease of explanation)
- : checks
- if all terms are 0: sum is 0
- any non-zero term: cause it to change
- at the end of protocol: evaluates
- suffices to evaluate
- 👨🏫in practice, this dominates the runtime
- outside of these: runs in time
- no. of variables
- performs field operations given
- even if there was no proof of correctness: same time
- suffices to evaluate
- (works over integers, for ease of explanation)
- Recall sum-check