Introduction
information
This is a poorly written note of ZKP MOOC
Introduction
information
This is lecture 1: Introduction and History of ZKP
Introduction and History of ZKP
Date: 2024-08-25 03:05:06
Reviewed:
Topic / Chapter: Introduction and History of ZKP
summary
❓Questions
Notes
Introduction
- classical proofs: Gauss, Euclid, Turing…
- e.g. Prime number proof
- ours: interactive proof
- w/ prover & verifier, as “algorithms”
- “efficiently” verifiable proofs
- aka “NP-proofs”
- msg {prover → verifier} is short
- of polynomial size in length
- time taken to proof: not considered
- of polynomial size in length
- and verifiable in a polynomial time
- i.e. time to compute
- example claim:
- : large prime
- proof 1: provides value of
- after interaction, knows:
- value of // revealed!
- after interaction, knows:
- example claim 2:
- : quadratic residue
- 👨🏫finding such number: hard
- proof 1: can simply provide
- verifier: compute
- after interaction, knows:
- value of
- example claim 3: two graphs are isomorphic
- proof:
- verification 1:
- iff
- such verification: hard
- after interaction, V knows:
- being isomorphic to
- isomorphism
- general form
- language set of strings
- NP language: s.t. in time some verifier can show:
- completeness: true claims have short proofs
- if : -long witness
- allows “honest provers” to convince
- soundness: false theorems have no proofs
- if :
- unable to convince wrong claim
- completeness: true claims have short proofs
- can we prove something without revealing information?
- yes!
- rather proves: “prove that I could prove it if I felt like it”
- and : knows nothing more than that claim is right
Paradigm shift
- interactive and probabilistic proofs
- interaction: verifier engages in an interaction w/ the prover
- 👨🏫could be mostly removed later
- randomness: verifier is randomized
- and tolerant to accept potential error w/ small probability
- e.g. smaller than Avogadro’s number
- interaction: verifier engages in an interaction w/ the prover
- Again, the idea:
- only transfers the claim (as knowledge)
- e.g. page w/ 2 colors
- flips the page “probabilistically” (e.g. flip if coin’s on head)
- V: sends the page
- P: interpret the event happened
- e.g. the coin was on head
- accepts the proof if it is right repeatedly
- provers
- : probability of accepting wrongly
- if repeat times:
- provers
- example: quadratic residue
- proof of existence of a pair
- prover: choose random s.t.
- s.t.
- sends
- after, by providing and , claim can be proven
- however: from and , can be computed
- which are respectively
- but: reveal of both are undesirable
- to convince: must be able to answer ANY ONE of two (but not answering both)
- verifier: chooses randomly
- verifier: accepts only when the prover’s submission is what he asked
- technically: when submission’s “square” is what he asked for
- if and he wanted that: yes
- or: if and he wanted that: yes
- all prover need to know: value of
- repeat: 100 times
- idea: many possible proofs are available
- prover: chooses one at random
- proof: made up of 2 parts
- which, is only meaningful if both are available
More
- formal definition
- is an interactive proof for , if is probabilistic time &
- completeness: : always accepts
- notation:
- soundness: if , for all cheating prover strategy, will not accept except for negligible probability
-
- : cheating prober
- for all polynomials
- growing very slowly (exponentially)
-
- for homework: just make sure:
- and show:
- (actually equivalent)
- Classes
- class of languages : all w/ interactive proof
- w/ verifier being in probabilistic polynomial time
- class of languages : all w/ interactive proof
what is zero knowledge?
- true statement: verifier cannot compute anything new
- for even malicious verifier
- after interaction, V learned:
- theorem being true, or
- a view of interaction
- i.e. transcript & coins V tossed
-
- probability distribution over coins of V and P
- the view gives V nothing new if:
- V could have simulated it its own
- w/ probabilistic distribution
- and two views are “computationally-indistinguishable”
- i.e. undistinguishable by external, poly-time distinguisher
- or: can’t tell if V is lying
- (aka simulation paradigm)
- V could have simulated it its own
- computationally-indistinguishability
- if no distinguisher can tell apart two probability distributions
- or:
- zero knowledge definition:
- for IP for , exists a PPT algorithm simulator s.t.
- : “may (very unluckily)” not run in polynomial time
- “expected” polynomial time
- : “may (very unluckily)” not run in polynomial time
- (when it’s true), following two are poly-time indistinguishable
-
- : technicality
- only effective for small
- : a ZK-IP if it is complete, sound, and zero-knowledge
- for any , even dishonest ones
- for IP for , exists a PPT algorithm simulator s.t.
- final def:
- IP is ZK for if PPT , PPT s.t.,
- IP is ZK for if PPT , PPT s.t.,
- Different types of ZK
- CZK: computationally indistinguishable distribution
- PZK: perfectly identical distributions
- SZK: statistically close distribution
example w/ QR
- example w/ QR
- (honest verifier) PZK
- simulator: picks random bit
- pick a random
- compute
- output (view):
- honest: checks
- key: not releasing initially
- dishonest verifier
- compute based on complex process
- yet: the view would be the same as simulator.
- simulator for baddie
- pick a random bit
- pick a random
- compute
- RUNS BAD Verifier (both are poly-time)
- if
- if was to be asked:
- output (view):
- else: repeat the whole process (50/50)
- if
POK
- prover: actually also proved
- “I can solve it (but won’t do it for you)”
- “knowledge”: can also be defined
- consider for poly-time relation
- if the knowledge can be gained by running program w/ multiple inputs:
- the algorithm has “knowledge”
- proof of knowledge (POK) for
- if PPT extractor algorithm s.t. , PPT outputs s.t.
- : may run repeatedly on the same randomness
- but may also run different questions each executions
- aka: rewinding technique
- as: one can “rewind” the algorithm to start from the same point
- ZKPOK on QR
- on input
- run prover & receive
- set verifier message to head (1), store
- rewind (to value), and runs tail
- gets
- output:
- ZKPOK on graph isomorphism
- produce random graph s.t. either one is available
- isomorphism from to
- isomorphism from to
- thus, isomorphism from
- verifier: randomly choose between two isomorphism
- proof:
- set
- claim:
- statement true: can correctly answer for either
- false: P(mistake)≥1/2
- and make it 1-1/2^k by repetition
- prove that it is a perfect ZK
- ZKPOK
- store
- rewind & get
- then output:
- produce random graph s.t. either one is available
- first application: identity theft
- Alice: wants to prove her identity over the net (insecure)
- to Bob: or Amazon
- password shouldn’t be stored: even as a an encryption
- Alice: wants to prove her identity over the net (insecure)
- solution: let’s say: password = hard theorem
- one who knows the answer: Alice
- ~= one who can pick up Excalibur: the Brave
- but Alice’s proof: must be ZKP
- one who knows the answer: Alice
- do all NP languages have ZK-IP?
- Yes
- if one-way functions exist, every L in NP has computational ZK-IP
- idea:
- show an NP-complete problem has a ZK-IP
- if a language is NP-complete: every string s can be reduced to a graph
- one way function → hiding & binding bit commitment protocol
- show an NP-complete problem has a ZK-IP
- Properties of bit commitment scheme
- hiding: the view (of ) is computationally indistinguishable
- key: must be randomized in order to keep it secure
- binding: probability of accepting different values are negligible
- hiding: the view (of ) is computationally indistinguishable
G3-colorable theorem
- common input graph:
- prover input coloring
- procedure
- prover: pic random permutation on colors and apply it on graph
- and commit for each
- permutation: prevents accumulation of knowledge
- verifier: select a random edge , and send it to prover
- prover: decommit colors
- decision: rejects if
- and accepts after iterations
- prover: pic random permutation on colors and apply it on graph
- ZK testing
- completeness
- honest prover: can always prove it & accepted
- soundness
- if is not 3-colorable, then
- for
- zk-ness
- easy to see informally
- messy to prove formally
- completeness
- honest verifier computational ZK
- choose challenge at random in advance
- for honest
- choose random edge in
- choose colors in s.t. at random
- and for all other , set
- simulated-view: commitments to edges
- and decommitting the challenge
- however: all except the challenge: the same color
- although computationally indistinguishable
- choose challenge at random in advance
- simulation for any verifier
- simulator on input and verifier for
- choose random edge
- generate commitments to colors as in honest simulation
- run on to obtain challenge
- ⇒ then output simulation as honest case
- if “all” iterations fail: output
- now: we haze many CZK examples as NP-languages
Protocol design applications
- can prover properties on without revealing
- only of
- as well as on relationship
- generally: a tool to enforce honest behavior in protocols w/o revealing any information
- idea: protocol players sends along w/ each next-msg, a ZK proof that
*next-msg* = Protocol(history h, randomness r)onhistory h & c=commit(r)- possible since s.t.
*next-msg* = Protocol(h,r) & c=commit(r)in NP
- possible since s.t.
- used in
- preventing identity theft
- computation delegation
- ??? nuclear disarmament, forensics
- ⭐Zcash: Bit Coin w/ privacy and anonymity
- ZK and verification dilemmas in the law
- interactive proof: also used in complexity theory
- can we do something in IP that traditional proof can’t?
- 🧑🏫 yes
- classical verification on proving non-isomorphic
- e.g. checking edge-by-edge
- takes time → efficient verification is impossible
- can we do something in IP that traditional proof can’t?
- in IP
- input:
- V: flip coin , pick random
- P: if is isomorphic to : then , else 1
- V: reject if
- accept after repetitions
- : learns whether graph of his choice is isomorphic to or
- to fix: V must prove to P in ZK that he knows isomorphism
- however: it’s not zero-knowledge for any (unless it’s honest)
- Fiat-Shamir: removal of interaction?
- given ideal hash
- can be replaced by
Highlights
- before IP: notion of proof was NP
- NP verification: sending solution (solution)
- Co-NP verification: impossible (0 solutions)
- number of solutions for a statement
- cannot be verified
- PSPACE: not known
- i.e. alternation of quantifier
- w/ IP: all can be done!
- PSPACE = IP
- arriver of the second prover: MIP (2020)
- can get unconditional ZK for all NP
- lead to PCP theorem
- and combined w/ quantum computing: and.. smth crazy
Introduction
information
This is lecture 2: Introduction and History of ZKP
Cornell Format
Date:
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Topic 1
Date:
Reviewed:
Topic / Chapter:
❓Questions
Notes
- Introduction to Modern SNARKs
- SNARKs
- SNARK: a succinct proof that a certain statement is true
- i.e. “short” and “fast” to verify
- e.g. solution itself: might not be short nor fast to verify
- zk-SNARK: revealing nothing about
- potentially: a single reliable PC can monitor supercomputers’ operation
- or: slow computer monitoring GPUs
- slow computer: like layer-1s
- SNARK: a succinct proof that a certain statement is true
- Blockchain applications 1
- outsourcing computation (not zk)
- L1: quickly verifies work of off-chain service
- e.g. scalability: proof-based rollups (zkRollup)
- off-chain service processes a batch of Tx
- L1 chain: verifies a succinct proof of correct processing
- e.g. bridging blockchains: Po-Consensus (zkBridge)
- enables transfer of assets from one chain to another
- proving to target chain that asset was locked in source chain
- outsourcing computation (not zk)
- Blockchain applications 2
- (requiring zk)
- private Tx on a public blockchain
- zk proof that a private Tx is valid
- compliance
- proof that a private Tx is compliant w/ banking laws
- proof that an exchange is solvent in zk
- also: non-blockchain applications exist
- e.g. fighting disinformation: C2PA
- camera: w/ embedded secret key
- and signs picture w/ location & timestamp
- metadata: can be confirmed
- problem: image post-processing
- disable further C2PA verification
- zk-SNARK solution
- laptop: w/
(Photo, Ops) - : proves that “I know a pair
(Orig, Sig)s.t.”Siga valid C2PA signature onOrigPhotois result of applyingOpstoOrigmetadata(Photo)==metadata(Orig)
- laptop verifies and shows metadata
- size: ≤ 1 KB, takes ≤ 10 ms in browser
- proof generation: takes a few minutes w/ sufficient HW
- parallelizable
- proof generation: takes a few minutes w/ sufficient HW
- proof: must be not interactable
- laptop: w/
- SNARKs
- What is SNARK
- Arithmetic circuits
- computation model: must be fixed to build SNARK
- let for
- finite field
- closed w/ addition & multiplication
- arithmetic circuits
- (n input w/ 1 output)
- directed acyclic graph, where
- internal nodes:
- inputs:
- defines: n-variate polynomial w/ evaluation recipe
- : no. of gates in
- interesting cases
- :
-
- gates (”small”)
- : output 0 if a valid ECDSA sig of
- structured vs. unstructured circuits
-
unstructured: w/ arbitrary wires
-
structured: build in layers, one circuit being repeated

- layer: aka VM
-
- NARK: Non-interactive ARgument of Knowledge
- applied arithmetic circuit
-
- : oublic statement in
- : secret witness in
- preprocessing: public params ()
- public param for prover / verifier
-
- prover:
- generate proof that
- verifier:
- preprocessing NARK: triple
- : description of circuit
- : accept / reject
- all alg. and adversary: w/ access to random oracle
- informal requirements
- complete: ⇒
- i.e. always accept if valid
- or: “knowledge sound”
- if accepts ⇒ “knows” s.t.
- and extractor can extract a valid
- optional: ZK: reveals “nothing new” about
- complete: ⇒
- trivial NARK:
- applied arithmetic circuit
- SNARK
- succinct preprocessing NARK
- same for
- : short
len($\pi$) = sublinear($|w|$)
- : fast to verify
time(V)= $O_{\lambda}(|x|$, sublinear($|C|$))
- i.e. anything better than NARK: technically SNARK
- however, strongly succinct NARK is:
len($\pi$) = $O_{\lambda}(\log |C|)$time(V)= $O_{\lambda}(|x|,\log(|C|))$- i.e. no time to even read circuit
- thus: preprocessing needed
- : summary of
- most SNARKs to be discussed: in constant time
- trivial SNARK: not SNARK
- long proof
- might be hard (and slow)
- : might be secret
- Preprocessing (setup)
-
-
setup types
- trusted setup per circuit
- run fresh for each circuit
- and must be kept secret
- if is learned: false statements can be proven
- generator: destroyed after task
- trusted but universal (updatable) setup
- secret : independent of
- (global param)
- one-time setup, secret
-
- deterministic
- can be repeated
- transparent setup
- : doesn’t use secret data
- trusted setup per circuit
-
significant progress
size of verifier time setup post-quantum Groth’16 200 Bytes 1.5 ms trusted per circuit no Plonk / Marlin 400 Bytes 3 ms universal trusted setup no Bulletproofs 1.5 KB 3 sec transparent no STARK 100 KB 10 ms transparent yes - prover time: almost
-
- Knowledge
- if accepts ⇒ knows s.t.
- if knows : we can “torture” to get
- formal knowledge
- is knowledge sound for if
- eff. adversary s.t.
- ,
-
- i.e. non-negl
- then eff. extractor s.t.
- i.e. if there is an efficient prover, then we can extract the knowledge
- Arithmetic circuits
- Building an eff. SNARK
- Building SNARK
- general paradigm: two steps
- a functional commitment scheme
- cryptographic obj
- a compatible interactive oracle proof (IOP)
- info. theoretic obj
- result: SNARK for general circuits
- a functional commitment scheme
- commitments scheme
- made of commit & verify
- must satisfy: binding & hiding property
- standard commitment
- :
com:=H(m,r) - : accepts if
com=H(m,r)
- general paradigm: two steps
- Functional commitment scheme
- given a family of functions
-
- sent to verifier
- verifier: sends
- prover: sends and
- proving that and
- a functional commitment scheme for
- : outputs public param
-
- binding & optional hiding (for zk-SNARK)
-
- accept / reject
- a SNARK for relation
- , , and
- four important functional commitments
- polynomial commitments
- commit to a univariate in
- multilinear commitments
- commit to multilinear in
- e.g.
- vector commitments (e.g. Merkle tree)
- commit to
- open cells:
- prove that th index is
- inner product commitments
- aka inner product arguments (IPA)
- commit to
- open an inner product
- polynomial commitments
- Polynomial commitments
- commit to a univariate in
eval: for public , prover can convince- and
- for verifier w/
evalproof size & verifier time:- few examples
- w/ bilinear groups: KZG’10 (trusted setup), Dory’20
- w/ hash functions only: based on FRI (long eval proofs)
- w/ elliptic curves: Bulletproofs (short proof, but verifier time being )
- w/ groups of unknown order: Dark’20 (slow)
- KZG’10: most widely used
- trivial commitment scheme: not a polynomial commitment
- let
- output
- eval: prover sends to verifier
- verifier accepts if and
- proof size & verification time: linear in
- let
- Useful observation
- for a non-zero
- for :
- aka SZDL lemma
- also holds for multivariate polynomials
- : total degree of
- has at most roots in finite field
- and possibilities for
- for :
- thus, suppose and
- then is negligible
- and if , for high probability
- suppose and
- let
- for : if
- ⇒ w.h.p.
- as
- ⇒ w.h.p.
- ⇒ simple equality test for two committed polynomials
- for a non-zero
- Equality test protocol
- interactive protocol
- prover:
- verifier: gives
- prover: computes ,
- and attaches proof for
- along w/
- and attaches proof for
- verifier: accepts if
- valid proof
- can be made non-interactive (Fiat-Shamir)
- for all public-coin IP
- prover: generates by its own w/
-
- ,
- sends
-
- compute itself as well
- not a zk-SNARK as , is revealed
- interactive protocol
- F-IOP
- goal: boost functional commitment
- ⇒ SNARK for general circuits
- let be arith. circuit and
- F-IOP: proof system that proves as follows
-
- oracles for functions in
- can be replaced into commitments
- proof
- prover: sends
- verifier: sends
- prover: sends
- verifier: sends
- … repeated t times
- and verifier: runs
- prover: sends
-
- properties
- complete: then
- knowledge sound: unable to fake knowledge
- goal: boost functional commitment
- Example poly-IOP
- ↔
- prover
-
- as , is a polynomial
- sends:
- verifier
- (public)
- query
- query
- compute
- accept if
- V accepts ⇒ w.h.p. ⇒
- kind of reversed logic
- Extractor:
- output by computing all roots of
- IOP Zoo
- ⇒ SNARKs for general circuits
- Poly-IOP (w/ Poly-Commit)
- Sonic
- Marlin
- Plonk
- Multilinear-IOP (w/ Multilinear-Commit)
- Spartan
- Clover
- Hyperplonk
- Vector-IOP (w/ Merkle)
- STARK
- Breakdown
- Orion
- ⇒ SNARK (non-interactive via Fiat-Shamir)
- SNARKs in practice
- programs: written in Domain-Specific Language
- Circom, ZoKrates, Leo, Cairo, Noir..
- compiles to SNARK friendly format
- circuit, R1CS, …, EVM byte code
- → SNARK backend prover (heavy computation)
- outputs
- programs: written in Domain-Specific Language
- Building SNARK
Introduction
information
This is lecture 3: Introduction and History of ZKP
Cornell Format
Date:
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Topic 1
Date: 2024년 7월 2일
Reviewed:
Topic / Chapter:
❓Questions
Notes
-
Programming ZKP
-
Programming ZKP
- converting idea into work
- programmer: idea → high-level language
- compiler: high-level language → R1CS
- focus of today
- setup: R1CS → param
- prove: param → ZKP
- verify: param * ZKP → {0,1}
- converting idea into work
-
ZKP basics
- ZKPs for a predicate
- prover knows
- verifier: knows
- proof : shows holds
- but not reveals
- what can be ?
- in theory: any NP problem
- e.g. : factorization of
- e.g. secret key for public key
- etc.
- in practice: arithmetic circuit over input
- ZKPs for a predicate
-
Arithmetic circuits (ACs)
- domain: prime field
- : a large (~255 bit) prime
- : integers
- (modular) operations:
- approach 1: as a systems of field equations
- e.g.
- e.g.
- approach 2: as circuits
-
directed, acyclic graph
-
nodes: inputs, gates, constants
-
edges: wires / connections
-
(for the same eg)
graph LR w_0[w_0] --> OPtimes_0([x]) w_0[w_0] --> OPtimes_0([x]) w_0[w_0] --> OPtimes_0([x]) OPtimes_0([x]) --> OPeq_0([=]) w_1[w_1] --> OPtimes_1([x]) w_1[w_1] --> OPtimes_1([x]) OPtimes_1([x]) --> OPeq_1([=]) x[x] --> OPeq_0([=]) x[x] --> OPeq_1([=])
-
- domain: prime field
-
Approach 3: Rank 1 Constraint Systems (R1CS)
- R1CS: format for ZKP ACs
- definition (linear combination)
- : field elements
- :
- : equations of form
- : affine combination of variables / constants
- examples
-
- ❌
-
- matrix definition
- : vector of field elements
- : vector of field elements
- : matrices
- holds when
- i.e. element-wise product
- each rows of : coefficients for each R1CS
- width: 1 more than no. of variables to include constants
-
Writing an AC as R1CS
-
example illustrated
graph LR w_0[w_0] --> OPtimes_0([x]) w_1[w_1] --> OPtimes_0([x]) w_1[w_1] --> OPtimes_1([x]) OPtimes_0([x]) --w_2--> OPplus_0([+]) OPplus_0([+]) --w_3--> OPeq_0([=]) x_0[x_0] --> OPplus_0([+]) x_0[x_0] --> OPtimes_1([x]) OPtimes_1([x]) --w_4--> OPeq_0([=]) -
procedure
- write intermediate s
- write equations
-
- ;
-
now: how to convert high-level to R1CS?
- R1CS: like assembly
- conversion from R1CS: w/ libraries, compilers, etc.
-
most zk products: built similarly
- high-level code → compiler / library → R1CS → ZK proof system
-
example: Zcash
- : definition of “spending money anonymously”
- circuit: involves
- Merkle tree
- Pedersen hash
- signatures
- spend logic
- etc.
- written in Bellman library ⇒ R1CS
- three tool types:
- HDL
- Library
- PL + compiler
- three tool types:
- R1CS: fed into Groth16 (runs on user computer)
-
-
-
Using an HDL
-
Circom basics
- Circom: Hardware Description Language
- ≠ programming languages
PL HDL Objects variables operations programs / func wires gates circuit / sub-circ Actions mutate variables call functions connect wires create sub-circuits - HDLs for Digital Circuits
- Verilog (dominate)
- System Verilog
- VHDL
- Chisel
- Circom: HDL for R1CS
- wires: R1CS variables
- gates: R1CS constraints
- circuit: does 2 things
- sets variable values
- create R1CS constraints
- Circom: Hardware Description Language
-
Circom: base language
-
example code
template Multiply() { signal input x; signal input y; signal output z; z <-- x * y; z === x * y; } component main {public [x]} = Multiply(); -
a
template: is a (sub) circuit -
a
signalis a wireinputoroutputas property
-
<--: sets signal values -
===: creates constraints- must be rank-1
- one side: linear; another: quadratic
-
<==: does both (shorthand) -
specify that this template is the
main- also which signals are public and which are not
- input: implicitly private
- output: implicitly public
-
-
Circom: metaprogramming language
-
example
template RepeatedSquaring(n) { signal input x; signal output y; signal xs[n+1]; xs[0] <== x; for (var i = 0; i < n; i++) { xs[i+1] <== xs[i] * xs[i]; } y <== xs[n]; } component main {public [x]} = RepeatedSquaring(1000); -
template arguments (fixed at compile time)
- e.g. length for signal arrays
-
variables
- mutable
- not signals
- evaluated at compile-time
-
loops
-
if statements
-
array accesses
-
-
Circom: witness computation & sub-circuits
-
guaranteeing non-zero
template NonZero() { signal input in; signal inverse; inverse <-- 1 / in; // not R1CS 1 === in * signal; // is R1CS } template Main() { signal input a; signal input b; component nz = NonZero(); nz.in <== a; // quits if a == 0 0 === a * b; // asking: is B zero? } -
idea: to ask whether there exists multiplicative inverse
-
<--: more general than=== -
componentshold sub-circuits- access inputs / outputs w/ dot-notation
-
-
-
Circom Tutorial
- Implementing sudoku
- : puzzle
- : solution
- : goal & rules
- for simplification: forcing only no-duplicates-in-a-row rule
- roadmap
- implement
notEqual(i.e. difference ≠ 0) - implement
Distinct(n)from not Equal - implement
Bits4orin % 16 === in - implement
OneToNiceby computingBits4onin-1Bits4onin+6
- implement
Sudokuby- check whether all numbers are in range
- check whether solution matches the puzzle
- check whether all numbers in the same row are distinct
- implement
- Implementing sudoku
-
Using a Library
-
Library for R1CS
- Circom key features
- direct control over constraints
- custom language
- can be good / bad
- alternative: library in a host language
- Rust, OCaml, C++, Go…
- key type: constraint system
- maintains state about R1CS constraints & variable
- i.e. value for variables &
- key operations
- create variable
- create linear combinations of variables
- add constraint
- maintains state about R1CS constraints & variable
- Circom key features
-
Pseudo-rust example
- variable creation
cs.add_var(p, v) -> idcs: constraint systemp: visibility of variablev: assigned valueid: variable handle
- linear combination creation
cs.zero(): returns the empty LClc.add(c, id) -> lc'id: variable (handle)c: coefficientlc' := lc + c * id
- adding constraints
cs.constrain(lc_a, lc_b, lc_c)- adds constraint
lc_a * lc_b = lc_c
- variable creation
-
Example code: Boolean AND
#![allow(unused)] fn main() { fn and(cs: ConstraintSystem, a: Var, b: Var) -> Var { let result = cs.new_witness_var(|| a.value() & b.value()); self.cs.enforce_constrant( lc!() + a, lc!() + b, lc!() + result, ); result } } -
Leverage language abstractions
-
e.g. using structs, operator overloading, etc.
#![allow(unused)] fn main() { struct Boolean {var: Var}; // i.e. & overloading impl BitAnd for Boolean { fn and(self: Boolean, other: Boolean) -> Boolean { // same as before Boolean {var: result} } } } -
example usage
#![allow(unused)] fn main() { let a = Boolean::new_witness(|| true); let b = Boolean::new_witness(|| false); (a & b).enforce_equal(Boolean::FALSE); } -
many different gadget libraries
libsnark: gadgetlib (C++)arkworks: r1cs-srd + crypto-primitives (Rust)Snarky(Ocaml)Gnark(Go)
-
-
Witness computation
- can perform arbitrary computations to generate witnesses
- more freedom as it’s general-purposed language!
#![allow(unused)] fn main() { let a = Boolean::new_witness(|| (4 == 5) & (x < y)); let b = Boolean::new_witness(|| false); (a & b).enforce_equal(Boolean::FALSE); }- closure / lambda
||: executed only during proving
- can perform arbitrary computations to generate witnesses
-
-
Arkworks Tutorial (Rust)
-
Using a Compiler
-
HDL & circuit libraries comparison
- differences:
- host language vs. custom language
- similarities
- explicit wire creation
- explicit constraint creation
- 👨🏫is it necessary?
- No! by creating a new language, we can avoid it!
- differences:
-
ZoKrates syntax
#![allow(unused)] fn main() { type F = field; def main(public F x, private F[2] ys) { field y0 = y[0]; field y1 = y[1]; assert(x = y0 * y1); } }-
struct syntax for custom types
-
variables: contain values during execution / proving
-
can annotate privacy
-
“assert” creates constraints
-
main function exists
-
other language features
- integer generics
- arrays
- variables
- mutable
- fixed-length loops
- if expressions
- array accesses
-
feature example
#![allow(unused)] fn main() { def repeated_squaring<N>(field x) -> field { field[N] mut xs; xs[0] = x; for u32 i in 0..N { xs[i + 1] = xs[i] * xs[i]; } return xs[N]; } def main (public field x) -> field { repeated_squaring::<1000>(x) } } -
short: no way to compute witnesses
-
all witnesses: must be provided as input
#![allow(unused)] fn main() { def main(private field a, public field b) { assert(a * b == 1) } }
-
-
-
-
ZoKrates Tutorial (~= Rust)
- Compilation
- compile:
zokrates compile -i root.zok - setup:
zokrates setup - witness computation:
zokrates compute-witness -a 1 0 0 2 1 2 1 2- or: [[1,0], [0,2]] and [[1,2],[1,2]]
- proof generation:
zokrates generate-proof - verification:
zokrates verify
- compile:
- Compilation
-
Overview of Prominent ZKP Toolchains
- A quick tour
-
toolchain type
- HDL: language for circuit synthesis description
- library: library for describing circuit synthesis
- PL + compiler: a language, compiled to a circuit
-
organized view
language type standalone? no yes circuit library (Arkworks) HDL (Circom) program PR (ZoKrates) -
pros and cons
type Circom Arkworks ZoKrates pros clear constraints elegant syntax clear constraints as expressive as Rust easiest to learn elegant syntax cons hard to learn limited abstraction (no types, etc.) need to know Rust few optimizations limited witness computation -
other toolchains
HDL Library PL + Compiler Circom Arkworks (Rust) ZoKrates Gadgetlib (C++) Noir Bellman (Rust) Leo Snarky (OCaml) Cairo PLONKish (Rust) -
timeline
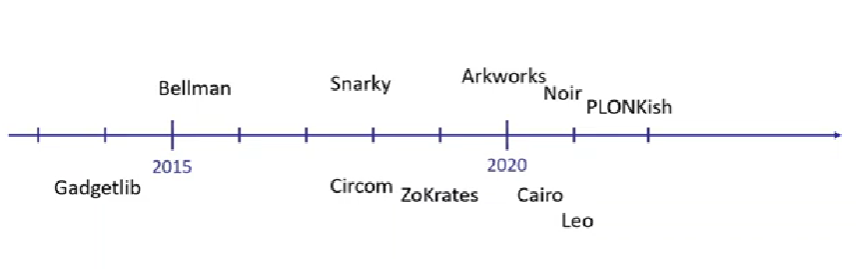
-
shared compiler infrastructure?
- source: (many PLs)
- target: R1CS, Plonk, AIR
- common techniques
- Boolean
- fixed-width ints
- variables
- mutation
- structures
- control flow
- optimization
- arrays
- 👨🏫can we build a library to create a PL for ZKP with this common ground?
- attempt: CirC
-
- A quick tour
Introduction
information
This is lecture 4: Introduction and History of ZKP
Date:
Reviewed:
Topic / Chapter: SNARKs via Interactive Proofs
❓Questions
Notes
- Interactive Proofs
- Motivation
- computation-limited verifier
- wants data analysis
- verifier: holds data summary
- queries to cloud provider w/ data
- or: “challenges”
- cloud provider: provides answer
- queries to cloud provider w/ data
- interactive proofs (formally)
- solves problem, tells the answer
- then conversation goes
- ’s goal: convince the answer is correct
- requirements
- completeness: an honest can convince
- (statistical) soundness: will catch ’s lie w.h.p.
- if soundness holds only against “eff” provers: then it is argument not proof
- solves problem, tells the answer
- computation-limited verifier
- Interactive proofs vs. arguments
- soundness vs. knowledge soundness
- soundness: accepts → s.t.
- knowledge soundness: accepts → “knows” s.t.
- 👨🏫stronger!
- standard soundness: meaningful even when knowledge soundness isn’t
- as there is no “natural witness”
- e.g. claims that output of ’s program on is 42
- reverse: prover claims he knows secret key for a certain BTC wallet
- or: preimage of hash that gives 0
- many “witnesses” exist
- public verifiability
- only convincing the party that is choosing random challenges
- others: can’t trust the proposed verifier
- if interactive: each run only convinces one party
- for public coin protocols: Fiat-Shamir is used
- to make it non-interactive
- only convincing the party that is choosing random challenges
- soundness vs. knowledge soundness
- Motivation
- SNARKs from Interactive Proofs
- SNARK example
- procedure
- : commits cryptographically to
- reveals “just enough” info on commitment to allow to run checks
- render non-interactive via Fiat-Shamir
- procedure
- SNARK example
- Review of Functional Commitments
- Functional commitments
- different types
- polynomial commitments
- to univariate
- multilinear commitments
- to multilinear
- vector commitments (e.g. Merkle trees)
- to
- open cells:
- polynomial commitments
- different types
- Merkle trees: the commitment
- uses: C.R. hash function
- opening proof size:
- example: univariate
-
- …
- to prove value , must provide
- , , ,
-
- notation
- Merkle-commits to all evaluations of
- upon request of , reveals all associated leaf along w/ opening info
- two problems
- no. of leaves:
- takes at least to compute commitment
- want time proportional to degree bound
- does not know has at most degree
- no. of leaves:
- Functional commitments
- Interactive Proof Design: Technical Preliminaries
- SZDL lemma
- FACT: let be univariate polynomials of degree at most
- then
- has at most zeros
- SZDL lemma: multivariate generalization
- let be -variate polynomials of total degree at most
- then
- using multivariate to lower the degree and make computation quicker
- FACT: let be univariate polynomials of degree at most
- Low-degree and multilinear extensions
- extension: given , a -variate polynomial over : extend
- if
- multilinear extensions: any function has unique multilinear extension (MLE)
- multilinear: polynomial has degree at most 1 in each var
- e.g. , but not in
- extension: given , a -variate polynomial over : extend
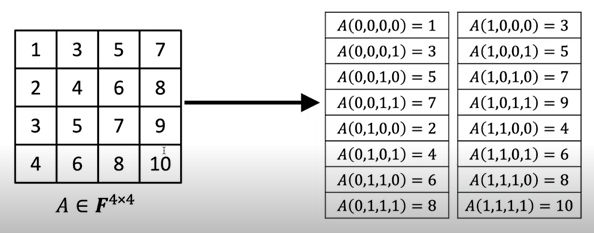
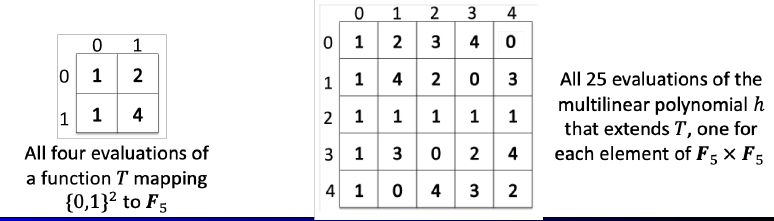
- Example
-
let s.t.
1 2 8 10 -
(multilinear extension)
-
- actually: quite similar to SoP approach!
1 2 3 4 5 6 8 10 12 14 16 18 15 18 21 24 27 30 22 26 30 34 38 52 29 34 39 44 49 56 - True as:
-
-
non-multilinear extension
1 2 3 4 5 6 8 10 12 14 16 18 13 16 19 22 25 28 16 20 24 28 32 36 17 22 27 32 37 42 - True as:
-
- Evaluating multilinear extensions quickly
- fact: given as input evaluations of a function
- -time algo to evaluate
- i.e. by listing all its values with manually
- sketch: using Lagrange interpolation
- define
- i.e. multilinear Lagrange basis polynomial corresponding to
- or: PoS, but from analog values of
- ( being digital)
- fact:
- , can be computed w/ field operations
- yields an -time also
- can reduce to time via DP
- fact: given as input evaluations of a function
- SZDL lemma
- Sum-Check Protocol
- Sum-check protocol
-
[LFKN90]
-
input: given oracle access to a -variate polynomial over field
- i.e. access to where
-
goal: compute the quantity
- idea: outsource the computation to prover so that it takes time instead of
-
👟Start: sends claimed answer
- protocol checks that:
-
👟Round 1: sends univariate polynomial claimed to equal
- i.e. output if prover was honest
-
checks that
- or:
-
if check passes: safe to believe that is the correct answer
- if believes
- i.e. check where
- can compute directly from ’s first message, not though
-
👟Round 2: ( sends and) recursively check that
- i.e. that
-
👟Round : ( sends and) check that
- : checks that
- by picking
-
general idea: checking only on first occurrence, trusting it there after
-
- Sum-check protocol
- Analysis of Sum-Check Protocol
- Completeness
- holds by design
- if sends the prescribed messages: all tests will pass
- Soundness
- if some other message was sent: rejects w/ probability of at least
- e.g. , ,
- then soundness error
- proof: by induction on no. of var
- base case: ; sends claims to equal
- picks at random, checks that
- if , then
- inductive case
- recall: ’s first message claimed to equal
- picks at random, (recursively) checks that
- if , then
- if , is left to prove a false claim in rec. call
- applies sum-check to variate
- by induction: convinces w/ probability at most
- base case: ; sends claims to equal
- summary: if , accepts at most
- Cost of the protocol
- total communication: field elements
- sends messages, each at univariate degree
- sends messages, each w/ 1 field element
- ’s runtime:
- ’s runtime (at most)
- total communication: field elements
- Completeness
- Sum-Check Protocol Application
- Counting triangles
- input:
- representing adjacency matrix of a graph
- desired output:
- fastest known algorithm: runs in matrix-multiplication time
- i.e. ~= (super linear time)
- IP: let verifier run in time (minimum possible)
- input:
- Protocol
-
protocol: view
-
: multilinear extension of
-
define polynomial
-
apply the sum-check protocol to compute
-
- Costs
- total communication:
- runtime:
- runtime:
- runtime: dominated by evaluating
- Counting triangles
- SNARK for Circuit-Satisfiability
-
SNARK for circuit-satisfiability
- : agreed on circuit over size and output
- claims to know s.t.
- let be empty for simplicity
- transcript for : assignment of a value to every gate
- is correct if it assigns gate values upon evaluating on a valid
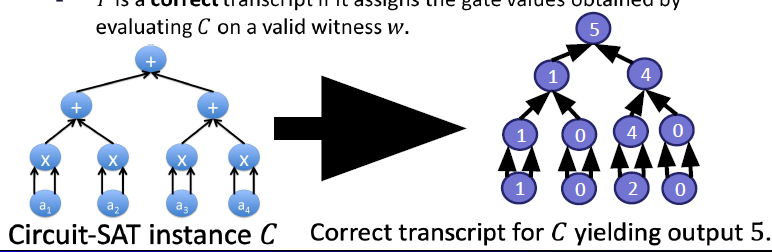
- : agreed on circuit over size and output
-
Transcript as a function
- with domain
- assign each gate in a ()-bit label and view as a function
- mapping gate labels to
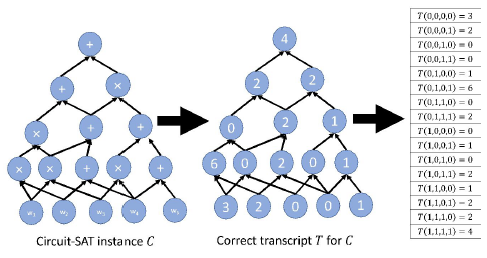
- and final output: always (last gate to be computed)
-
- Polynomial IOP Underlying the SNARK
-
Polynomial IOP
- ’s first message is a ()-variate polynomial claimed to extend a correct transcript
- i.e.
- : needs to check this, but only able to learn few evaluation of (not )
- ’s first message is a ()-variate polynomial claimed to extend a correct transcript
-
Intuition on
- : distance-amplified encoding of
- domain of :
- but domain of : much larger ()
- 👨🏫small difference in → vast difference (almost all) in extension
- due to distance-amplifying nature
- by Schwartz-Zippel
-
Two-step plan
- step 1: given any ()-variate polynomial , identify a related ()-variate polynomial s.t.
- extends a correct transcript ↔
- or: “vanishing” over Boolean hypercube
- i.e. if is not a correct transcript:
- ~= abstraction of messy structure?
- also: to evaluate at any input: evaluating at 3 inputs are enough
- extends a correct transcript ↔
- step 2: design an IP to check
- in which only needs to evaluate at one point
- step 1: given any ()-variate polynomial , identify a related ()-variate polynomial s.t.
-
Sketch
- step 1 sketch: define via:
- : gets 3 Boolean vectors in input
- returns 1 iff is addition gate and 2 neighbors are
- else 0
- : gets 3 Boolean vectors in input
- returns 1 iff is multiplication gate and 2 neighbors are
- else 0
- properties
-
- if is label computing sum of
-
- if is label computing multiplication of
- otherwise
- computation: can be outsourced to as it only depends on wiring structure, and thus being able to be committed
-
- step 2: how to check
- by evaluating at a single point?
- if were a univariate polynomial
- and we need to check that vanishes over some set , not
- fact: ↔ is divisible by
- : vanishing polynomial for
- 🧑🎓kind of trivial
- polynomial IOP
- sends a polynomial s.t.
- checks this by picking a random and checking
- step 1 sketch: define via:
-
Actual protocol
- above: not works as is not univariate
- computing (finding ) is expensive
- in final SNARK: it would be applying poly-commit to additional polynomials
- Marlin, PlonK, Groth16 does this, though
- solution: use the sum-check protocol
- handles multivariate polynomials
- doesn’t require to send additional large polynomials
-
- Polynomial IOP for Circuit-Satisfiability
- Recall sum-check
- goal: compute the quantity (all sum)
- proof length: roughly total degree of
- no. of round:
- time: ~= time to evaluate
- not necessarily revealing info on as long as it knows for random
- General idea
- (works over integers, for ease of explanation)
- : checks
- if all terms are 0: sum is 0
- any non-zero term: cause it to change
- at the end of protocol: evaluates
- suffices to evaluate
- 👨🏫in practice, this dominates the runtime
- outside of these: runs in time
- no. of variables
- performs field operations given
- even if there was no proof of correctness: same time
- suffices to evaluate
- (works over integers, for ease of explanation)
- Recall sum-check
Introduction
information
This is lecture 5: The Plonk SNARK
Building Eff. SNARK
Date: 2024-08-28 21:09:49
Reviewed:
Topic / Chapter: Building Eff. SNARK
summary
❓Questions
Notes
Overview
- General idea
- poly-commit + poly-IOP ⇒ SNARK for general circuits
- Polynomial commitment review
- commits to
eval: for public , prover can convince, for committed ,- ⭐ and
- : with
- proof size & verif time:
KZG poly-commit scheme (2010)
- ⭐group:
- or order , and is cyclic
- setup()→
- delete (trusted setup)
- ⭐commit()→ where
- use to compute
- 👨🏫is binds, but not hides!
-
- ⇒
Evaluation
- commit(
- and
- ↔ being root of
- ↔ divides
- ↔ s.t.
- i.e. divisible
- ⭐: compute , and
- ⭐⭐
- proof size:
- 👨🏫computationally expensive!
- accepts if
- i.e.
- if agrees: true w.h.p.
- : computed using “pairing” from from
- i.e.
KZG poly-commit scheme
- generalization
- can commit to -variate polynomials
- batch proofs
- assume has
- proving for ,
- batch proof : only one group element!
- linear time commitment
- two ways to commit
- coefficient representation:
- ⇒computing
- takes time
- ⇒computing
- point-value representation:
- computing naively: construct coeffs.
- ⇒ time w/ Num. Th. Transform
- point-value representation: better
- Lagrange interpolation:
-
- =1 if , 0 otherwise
- idea: transform into Lagrange (linear map)
- now:
- ⇒ in time, not
- multi-point proof generation
- w/
- and
- if needs
- naive: takes , proofs each taking
- Feist-Khovratovich (2020):
- if a multiplicative subgroup: time
- else:
Dory polynomial commitment
- difficulties w/ KZG: trusted setup for ,
- Dory:
- transparent setup: no secret randomness in setup
- : single group element (independent of )
evalproof size: group elements- verify time: constant in KZG
evalverify time: ; prover:- verify time: constant in KZG
- Dory:
PCS applications
- e.g. vector commitment (replacing Merkle trees)
- : vector
- interpolate poly
- sends to
- : asks to prove ,
- : generate eval proof that
- w/ KZG: a single group element
- shorter than Merkle proof
- sends
- : accept / reject
Proving Properties of Committed Polynomials
Date: 2024-08-28 21:10:30
Reviewed:
Topic / Chapter: Proving Properties of Committed Polynomials
summary
❓Questions
Notes
Topic 1
- Proving Properties of Committed Polynomials
- Meaning of proof
- and
- goal: convince that satisfy some properties
- proof system (IOP)
- :
- :
- : query: for
- :
- Example: polynomial equality testing
- , (i.e. is negl.)
- let
- for , then w.h.p.
- simple equality test
- proof as IOP: ↔ query and at
- procedure (after compile)
- w/
- query
- learns them
- sends and
- : accepts if valid s and
- Example: polynomial equality testing w/ KZG
-
- ⇒ can tell if on its own (no need extra computation)
- however: needed to test equality of “computed polynomials”
- e.g. w/
- and testing
- required prover to give values at
- in this case: complete and sound if is negl
-
- Important proof gadgets for univariates
- let and
- let ,
- with
- goal for eff. Poly-IOP: following
- task 1:
ZeroTest- prove that is identically zero on
- task 2:
SumCheck- prove that
- task 3:
ProdCheck- prove that
- task 1:
- Vanishing polynomial
- let and
- vanishing polynomial of :
-
- i.e. 0 for everywhere in
-
- being multiplicative subgroup of : important
- let primitive th root of unity
- i.e.
- if
- then
- for , evaluating takes field operations
ZeroTeston ()- lemma:
- ⭐:
- if , then leads to “clean” polynomial
-
- it not polynomial: cannot commit
- :
- query at
- accept if
- 👨🏫 to be computed by !
- complete & sound assuming is negl.
- time: and 2 (or: one) poly queries
- time: computing and committing
- or
ProductTeston ()- set be degree- polynomial:
- ,
- for
- example
-
- (supposedly)
- and
- , including
- ,
- lemma: if and
- ⇒
- (unoptimized) procedure
-
- should be 0 on
- set
- leads to clean polynomial if
- : sends
- : query at
- also at , and at
- learns
- : accepts if and
- proof size: 2 commits, 5 eval. = 3 groups
- time: (for )
- time: (for quotient)
- set be degree- polynomial:
- Approach on rational functions
- Meaning of proof
The PLONK IOP for General Circuits
Date: 2024-08-28 21:10:53
Reviewed:
Topic / Chapter: The PLONK IOP for General Circuits
summary