COMP 2711H: Lecture 20

Date: 2024-10-16 22:28:14

Reviewed:

Topic / Chapter: Stable Matchings and Graph Coloring

summary

❓Questions

Notes

Stable Matchings

Problem reduction
- given: bipartite graph $G$
- return: maximum matching $M$
- can we: leverage the fact that the graph is bipartite?
- idea: convert bipartite graph to max flow problem
  1. let all edge between $L, R$ to be directed $L \to R$
  2. add a source $s$ , connect to all vertex $\in L$
    - add a sink $t$ , connect to all vertex $\in R$
    - for all edge: direction is left to right
    - all with same capacity
  - claim: maximum flow in this new graph, $H$ : gives size of maximum matching in $G$
- strategy: prove that two are $\leq$ to each other
- assume: original matching exists in $G$
  - then: as no two endpoint overlaps, one can create a flow based on it
    - without going over the capacity
  - for any matching, there is a flow of same size (= sharing common edges)
    - thus max matching <= max flow
- the other way: a flow exists in $H$
  - where unit: $\in {0, 1}$
  - and consider: only flow / edge in bipartite points
    - all edge w/ flow = 1: makes a corresponding matching
  - as capacity of all edge: 1, no valid flow can have any conjunction (e.g. $u \to v, w \to v$ )
  - max matching >= max flow
- 👨‍🏫 overall idea: reduction
  - algorithm solving one problem: can solve another problem
    - regardless of details of algorithm
  - we: reduced maximum flow into maximum matching
    - 👨‍🏫 you can somewhat claim: max flow is a harder problem
Stable matchings
- e.g. $n$ man and $n$ women
- want: a perfect 1-to-1 matching
- problem: everyone has preferences
  - e.g. every woman $w_{i}$ : has a preference - permutation of $n$ man
  - same for man
- all: willing to marry
- suppose: $M$ is a perfect matching (all men & women: matched)
  - and $m_{i}, w_{j}$ : not matched together
- pair $(m_{i}, w_{j})$ : unstable if
  - $m_{i}$ prefers $w_{j}$ over current spouse
  - $w_{j}$ prefers $m_{i}$ over current spouse
- matching: stable if there are no unstable pairs
- theorem: there is always a stable perfect matching
- typical existence proof in graph: elaborate an algorithm finding solution
  - and prove correctness of the algorithm
Stable matching algorithm
- algorithm: of several iterations
- for every iteration:
  - all man propose to a most preferred woman
    - (who has not rejected him so far)
  - if: every woman has exactly one proposal $⟹$ they all accept; return
  - else: every woman w/ more than one proposal $⟹$ reject all except the most preferred one
    - yet: doesn't "accept" the top proposer as well
      - maybe tomorrow: she won't get any propose otherwise!
- algorithm: results in a stable perfect match!
Proof of correctness
- algorithm: terminates as
  - list of woman a man is willing to propose: shrinks
  - total sum on size of all list of woman-to-propose: decreases every time
    - yet: it can't go down below 0 ( $n$ to be precise)
- background
  - from man's PoV: preference is going down
    - from woman's PoV: preference is going up (better man might get rejected and come down)
  - no. of man not getting rejection: increases
- proof by contradiction
  - suppose $(m_{i}, w_{j})$ is unstable pair
    - $m_{i}$ prefers $w_{j}$ over current (e.g. $w_{i}$ )
    - and similarly so
  - it's impossible as: $m_{i}$ should have proposed to $w_{j}$ before
    - yet: it was rejected by $w_{j}$
      - which means: $w_{j}$ had a better option at the point
        
        $w_{j}$ 's current spouse: must be at least better than the previous optimal option
  - thus: algorithm always produces stable perfect matching

Graph Coloring

Graph coloring
- given graph $G$ : a proper coloring w/ $k$ colors: a function
  - $c : V \to {1, 2, \dots, k}$
  - s.t. for every edge $e \in E$ : two endpoints of $e$ w/ different color
- definition: doesn't matter whether edge is unidirectional or bidirectional
- chromatic number $χ (G)$ : minimal number of colors
  - needed to properly color $G$
- bipartite graph $⟺$ two-colorable
- independent set: $I \subseteq V$ s.t. no edge with both endpoints in $I$
- clique: $C \subseteq V$ s.t. $\forall u, v \in C, {u, v} \in E_{C}$
  - opposite of IS
  - complete subgraph?
- smallest IS/ clique: empty / one-vertex set
- question: can we cover any graph?
  - 👨‍🏫 is the graph is simple - if there is no loop!
  - having multiple edge between two nodes: doesn't matter
- let: $α (G)$ be size of a largest IS
- let: $ω (G)$ be size of a largest clique
Theorems
- theorem: $χ (G) \geq ω (G)$
  - somewhat obvious, as:
  - there must be $ω (G)$ colors for largest clique alone
- theorem: $χ (G) \geq \frac{n}{α ( G )}$
  - $α (G)$ : size of an largest IS
  - proper $k$ coloring: w/ $k$ groups
    - thus $k \cdot α (G) \geq n$
    - as each group: at most $α (G)$ elements
    - then: $α (G) \geq n / k$
  - finally: let $k$ be chromatic number
- theorem: $χ (G) \leq n = ∣ V ∣$
  - e.g. complete graph
- theorem: suppose $G$ : graph w/ maximum degree $Δ$
  - $χ (G) \leq 1 + Δ$
  - algorithm: greedy coloring
    - pick a vertex: color it w/ smallest color possible
      - (i.e. not used with its neighbors)
    - repeat until all are colored
    - doesn't return an optimal color
  - above algorithm: colors w/ at most $1 + Δ$
    - as $i \in V$ : at most $Δ$ neighbors
      - and thus (even if its neighbors have all distinct colors):
        
        $i$ can be colored with at most $Δ + 1$ color
  - 👨‍🏫 no particular better upper bound
    - e.g. a triangle / odd cycle: max degree being $2$
      - and it requires $1 + 2 = 3$ colors
      - same for a complete graph: max degree $n - 1$ , $χ (G) = n - 1 + 1 = n$
  - exists a theorem: only graphs requiring $1 + Δ$ colors are odd cycles / complete graphs
- finding a better order of coloring
  - first: sort vertices w/ degree in non-increasing order
    - then: color it the same way as primary school method above
- theorem: let $G$ a graph w/ degree seq. $d_{1} \geq d_{2} \geq \dots \geq d_{n}$
  - $χ (G) \leq 1 + max_{i} min {d_{i}, i - 1}$
  - 👨‍🏫 many theorems in this area: derived from analysis of algorithm (solution)
  - assign $d_{1}$ color 1
    - then assign $d_{2}$ color 1 if $d_{1}$ is not its neighbor, 2 otherwise
  - on $d_{i}$ : no. of colored neighbors $\leq d_{i}$
    - as we colored total of $i - 1$ items previously: also $\leq i - 1$
    - thus: no. of colored neighbors $\leq min {d_{i}, i - 1}$
    - then $c (v_{i}) \leq min {d_{i}, i - 1} + 1$
  - finally, largest color used (not necessarily optimal) is
    - $\leq 1 + max_{i} min {d_{i}, i - 1}$
Cartesian product
- suppose $G, H$ : graphs
  - Cartesian product of two, aka $G □ H = (V_{G} \times V_{H}, E_{G □ H})$
  - rule: $(u, v) \to (u^{'}, v^{'})$ if:
    - $u = u^{'} \land v \to v^{'} \in E_{H}$ or:
    - $u = u^{'} \land v \to v^{'} \in E_{G}$
- simple example: grid
  - for following $G, H$

---
      title: G, H
      ---
      graph LR
      1((1))-->2((2))
      2-->3((3))
      a((a))-->b((b))

- then <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal">G</span><span class="mord amsrm">□</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span></span></span></span>:

graph LR
      1a((1,a))-->2a((2,a))
      2a-->3a((3,a))
      1b((1,b))-->2b((2,b))
      2b-->3b((3,b))
      1a-->1b
      2a-->2b
      3a-->3b

literally, a grid
Theorem
- theorem: $χ (G □ H) = max (χ (G), χ (H))$
  - Cartesian product: cannot have less coloring than operands
    - as it's some sort of copy / repeat
  - suppose: $χ (G) = k, χ (H) = t$
    - and $k \geq t$
  - $c_{G} : V_{G} \to {0, 1, \dots, k - 1}$
  - $c_{H} : V_{H} \to {0, 1, \dots, t - 1}$
  - $c : V_{G} \times V_{H} \to {0, \dots, k - 1}$
    - $(u, v) \mapsto (c_{G} (u) + c_{H} (v)) % k$
  - example
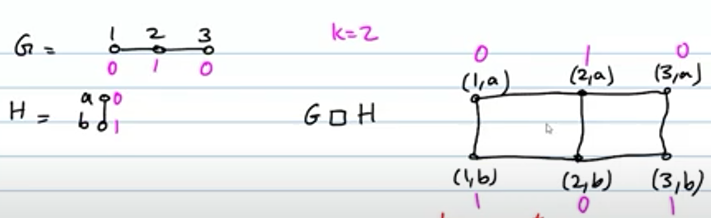
  - and this is a proper coloring in general, as in either case of the rule:
    - $u = u^{'} \land v \to v^{'} \in E_{H}$ or:
    - $u = u^{'} \land v \to v^{'} \in E_{G}$
  - we are assigning a new color
  - case 1: $u = u^{'} \land v \to v^{'} \in E_{H}$
    - $c (u, v) \mapsto (c_{G} (u) + c_{H} (v)) % k$
    - $c (u, v^{'}) \mapsto (c_{G} (u) + c_{H} (v^{'})) % k$
    - and there is an edge $v \to v^{'}$ , thus $c_{H} (v) \neq = c_{H} (v^{'})$
      - as sum are different (and $k \geq t$ ), $mod k$ is different, too
  - case 2: can be done similarly
    - $u, u^{'}$ instead of $v, v^{'}$
  - finally: it's a valid coloring

COMP 2711H: Honors Discrete Mathematical Tools for Computer Science