Introduction
information
These are my notes on COMP 2711H: Honors Discrete Mathematical Tools for Computer Science
- Lecture 1
- Lecture 2
- Lecture 3
- Lecture 4
- Lecture 5
- Lecture 6
- Lecture 7
- Lecture 8
- Lecture 9
- Lecture 10
- Lecture 11
- Lecture 12
- Lecture 13
- Lecture 14
- Lecture 15
- Lecture 16
- Lecture 17
- Lecture 18
- Lecture 19
- Lecture 20
- Lecture 21
- Lecture 22
- Lecture 23
- Lecture 24
- Lecture 25
- Lecture 26
- Lecture 27
- Lecture 28
- Lecture 29
- Lecture 30
- Lecture 31
- Lecture 32
- Lecture 33
- Lecture 34
- Lecture 35
- Lecture 36
- Lecture 37
- Lecture 38
Course information
- Course code: COMP 2711H
- Course title: Honors Discrete Mathematical Tools for Computer Science
- Semester: 24/25 Fall
- Credit: 4
- Grade: A-F
- TMI
- Prerequisite: Level 5* or above in HKDSE Mathematics Extended Module M1/M2; OR grade A- or above in MATH 1014; OR grade B+ or above in MATH 1020 / MATH 1024
Description
This course is an advanced (honors) version of "COMP 2711: Discrete Mathematical Tools for Computer Science" which provides a much more in-depth treatment of a wide variety of important mathematical concepts that form the theoretical basis of modern computer science.
Discrete mathematics needed for the study of computer science: sets, functions, propositional logic, predicate logic, rules of inference, proof techniques, pigeonhole principle, basic and generalized permutations and combinations, binomial coefficients, inclusion-exclusion principle, probability theory, Bayes theorem, expectation, variance, random variables, hashing, cryptography and modular arithmetic, Euclid’s division theorem, multiplicative inverse, divisibility, RSA cryptosystem, Chinese remainder theorem, mathematical induction, strong induction and well-ordering property, recursion, recurrence relations, graph representation, isomorphism, connectivity, Eulerian paths, Hamiltonian paths, planarity, graph coloring. Gentle introduction to many discrete mathematical concepts that will appear later in more advanced computer science courses.
Topics covered
- Proofs and Reasoning: Propositional Logic, First-order (Predicate) Logic, Quantifiers, Proof by contradiction, Mathematical Induction, the Pigeonhole Principle, the Invariant Principle, the Extremal Principle, ...
- Set Theory: ZMC, Peano's Axioms, Dedekind Cuts, Relations, Functions, Ordinals and Cardinals, Russel's Paradox, ...
- Enumerative Combinatorics: Rules of Sum and Product, Permutations and Combinations, Inclusion-Exclusion, Catalan and Stirling Numbers, Generating Functions, Recurrence Relations, Double Counting, ...
- Probability Theory: Discrete and Countable Probability Spaces, Axiomatic Probability Theory, Measure Functions, Lebesgue Integrals, Conditional Probability, Independence, Random Variables, Bayesian Reasoning, Expectation, Stochastic Processes, Markov Chains, Markov Decision Processes, ...
- Number Theory: Divisibility, GCD, LCM, Primes, Congruence, Chinese Remainder Theorem, Theorems of Fermat, Euler and Wilson, Quadratic Reciprocity Law, the RSA and El-Gamal Cryptosystems, ...
- Graph Theory: Adjacency, Walks, Paths, Cycles, (Strong) Connectivity, Distance, Trees, Spanning Trees, Bipartite Graphs, Matchings, Shortest Paths, ...
- Game Theory: Combinatorial Games, Sprague-Grundy Theorem, Normal Form (Nash) Games, Nash Equilibria, Correlated Equilibria, Infinite Games on Graphs, ...
My section
- Section: L1 / T1
- Time:
- Lecture: MoWe 09:00AM - 10:20AM
- Tutorial: Mo 06:00PM - 06:50PM
- Venue:
- Lecture: Rm 2465, Lift 25-26
- Tutorial: Rm 4620, Lift 31-32
- Instructor: Amir Goharshady
- Email: [email protected]
- Teaching assistants
- Xuran Cai ([email protected])
- Zhaorun Lin ([email protected])
Grading scheme
| Assessment Task | Percentage |
|---|---|
| Mid-Term | 30% |
| 4 x HW | 40% |
| Final Exam | 30% |
- Resubmission for HW possible
Required texts
- Concrete Mathematics: A Foundation for Computer Science, by Ronald Graham, Donald Knuth, and Oren Patashnik
Optional resources
- Discrete and Combinatorial Mathematics by Grimaldi
- Concrete Mathematics by Knuth et al
- Principles and Techniques in Combinatorics by Chen and Meng
- A First Course in Probability by Ross
- Elementary Number Theory by Burton
- Set Theory: A First Course by Cunningham
- Introduction to Graph Theory by West
- Algorithmic Game Theory by Nisan and Roughgarden
- Problem Solving Strategies by Engel
- 102 Combinatorial Problems by Andreescu and Feng
- Winning Ways for Your Mathematical Plays by Berlekamp et al
- Reading materials
COMP 2711H: Lecture 1
Date: 2024-09-01 23:02:24
Reviewed:
Topic / Chapter: Propositional Logic
summary
❓Questions
- Is there any practical difference between logic / boolean algebra?
- Is Boolean algebra "algebra" because we have XYZ?
Notes
Introduction to the Course
-
COMP 2711H
- 👨🏫Honors, so we will put infinite pressure on you HAHA
- 0 coding, 100% theoretical
- this session: easy (unlike others)
- ~50%: have A's
- but thou shalt suffer before getting it!
- talking about basics: proof, proposition, set of natural numbers
- 👨🏫Honors, so we will put infinite pressure on you HAHA
Introduction to Propositions
-
Propositional logic
- proposition any statement that can be true / false (not both)
- 👨🏫or 1 or 0, as we are CS PPL
- if you can't assign Boolean value: not a statement
- e.g. "close the door" not boolean
- usually using for var. names
- atomic proposition prop. that can't be further broken down
- for combination: use operators like ("neg")
- and we often draw truth table to represent the value
- proposition any statement that can be true / false (not both)
-
Logical operators
-
negation: or
-
"it is not the case that "
- read as "not "
-
(!p) ? 1 : 0 -
always opposite of
1 0 0 1 -
examples
- "Prof. Amir uses Kali Linux for his desktop"
- "Prof. Amir doesn't use Kali Linux for his desktop"
-
-
disjunction:
-
" or "
-
(p || q) ? 1 : 0 -
0 only if both and are 0
1 1 1 1 0 1 0 1 1 0 0 0
-
-
conjunction:
-
" and "
-
(p && q) ? 1 : 0 -
1 only if both and are T
-
👨🏫 logical operator: kind of "promise" on condition
1 1 1 1 0 0 0 1 0 0 0 0
-
-
exclusive or (xor):
-
1 when exactly one of and is T
- 0 otherwise
-
((p && !q) || (!p && q)) ? 1 : 0- or:
(p ^ q) ? 1 : 0(bit-wise though)
1 1 0 1 0 1 0 1 1 0 0 0 - or:
-
-
implication
-
cond. state.:
- = prop. "if then "
-
: hypothesis / premise
-
: conclusion / consequence / implication
-
(!p || (p && q)) ? 1 : 0 -
👨🏫: any connection in : not needed
- simply depending on its values
-
👨🏫: also, kind of promise
- "if you are in classroom 2456, then you are Y1 student"
-
can be combined, like:
1 1 1 1 0 0 0 1 1 0 0 1 -
examples
- if the moon is made of green cheese, then I have more money than Bill Gates
- 👨🎓 as the hypothesis is false, the true value of conclusion doesn't matter
- 👨🎓 you broke the promise (more like, premise) first!!!
- if the moon is made of green cheese, then I have more money than Bill Gates
-
-
👨🏫 dual
- let be a statement
- is the statement obtained by following replacement
- example
-
-
Conditional statement
-
necessary / sufficient conditions
- if , then
- : sufficient condition of
- : necessary condition of
- examples
- if I am elected, then taxes will be lowered
- if elected: sufficient to know "tax will be lowered"
- if not "tax will be lowered" it must be that I am not elected
- other ways for
- if , then
- if
- when
- implies
- follows from
- is a sufficient condition for
- is a necessary condition for
- only if (falsity of : implies falsity of )
- if , then
-
converse, contrapositive
-
(below: of )
-
converse:
-
contrapositive:
-
inverse:
-
: equivalent to its contrapositive
T T T T T F F F F T T T F F T T
-
-
bi-conditional statement
-
bicon. state.:
- = prop. " if and only if "
- or: iff
-
T when and have the same truth value
- or
-
equivalent
- if and only if
- iff
- is "necessary and sufficient" for
- if then , and conversely
T T T T F F F T F F F T
-
-
Proof / Propositional Equivalence
-
Tautology and contradiction
- tautology: compound proposition, that is always true
- no matter values of the prop. vars in it
- 👨🏫: to proof: to show that certain statement is a tautology
- no matter values of the prop. vars in it
- contradiction: compound proposition, that is always false
- contingency: compound proposition that is neither a tautology nor a contradiction
- example
- is a tautology
- as well as
- as premise: always 0
- is a contradiction
- is a contingency
- is a tautology
- tautology: compound proposition, that is always true
-
Boolean algebra
- conjunction, disjunction, or negation: can be implemented in hardware easily
- 👨🏫 but, how can gates output true when all conjunctions are false?
- for simplicity, just imagine there is an extra power line
- 👨🏫 but, how can gates output true when all conjunctions are false?
- conjunction, disjunction, or negation: can be implemented in hardware easily
graph TD;
OR(( ∨ )) --> c_1[ ];
a_1[ ] --> OR;
b_1[ ] --> OR;
AND(( ∧ )) --> c_2[ ];
a_2[ ] --> AND;
b_2[ ] --> AND;
NOT(( ¬ )) --> c_3[ ];
a_3[ ] --> NOT;
-
let's build a simple adder!
- bit 0 adder:
- : defined as
- read as, "XOR"
- carry:
- bit 1:
- 👨🎓use 2611 knowledge
- 👨🏫: one thing you can't ask: "where will this course be useful?"
- bit 0 adder:
-
Logical equivalence
- compound prop. always having the same truth values: logically equivalent
- i.e. is a tautology
- notation: (or )
- : not a logical operator
- : not a compound prop., but a statement!
- that is a tautology
- example:
- 👨🎓 you can use truth table to compare! (manual)
- use of
- : denotes logical equivalence, regardless of var. values
- : binary logical operator
- : not used on propositions
- only on two mathematical quantities
- compound prop. always having the same truth values: logically equivalent
-
Propositional equivalences
- 👨🏫 many algebraic rules also work here!
- consider as addition, and as multiplication
major equivalences
Name Equivalence Identity laws Domination laws Idempotent laws Double negation laws Commutative laws Associative laws Distributive laws De Morgan's laws Absorption laws Negation laws Involving cond. states Involving bicond. states. - 👨🏫 many algebraic rules also work here!
-
Examples
- Use De Morgan's laws to express the negations of "Alice will send a secret message or Bob will send a secret message" and "today is Saturday and today is a holiday".
- Alice & Bob
- := Alice will send a secret message
- := Bob will send a secret message
expr:=expr==- = "Alice will NOT send a secret message and Bob will NOT send a secret message"
- Today is...
- := today is Saturday
- := today is a holiday
expr:=expr==
- Alice & Bob
- Show that and are logically equivalent by developing a series of logical equivalences.
- Show that and are logically equivalent by developing a series of logical equivalences.
- =
- Show that is a tautology by developing a series of logical equivalences.
- Use De Morgan's laws to express the negations of "Alice will send a secret message or Bob will send a secret message" and "today is Saturday and today is a holiday".
Rules of Inference
-
Rules of inference
-
theorem: statement that is always true (or: is a tautology)
-
we can write theorem as
-
better, we can define proof
- you can either fill in size table...
- or: you use "inference" from existing tautology
-
proof for is
- a sequence of statements
-
s.t. for each , either is true
- for some
- i.e. the premise
- is a tautology
- i.e. can be implied from prev. statements
- for some
-
👨🏫 "one rule is actually enough"
- but we introduce multiple for now
-
-
Rules
- modus ponens
- thereafter, you can use as a tautology
- or: " is a tautology"
- 👨🏫 just another way of writing a tautology!
- 👨🏫 the actual, only real rule here
- syllogism
- or: "" is a tautology
- modus tollens
- modus ponens
COMP 2711H: Lecture 2
Date: 2024-09-02 17:34:27
Reviewed:
Topic / Chapter: Predicate Logic and Peano's Axioms
summary
❓Questions
- Does predicate / logic have much thing to do with (3-)SAT?
- 👨🏫 No, that's more of an algorithm...
Notes
Rules of Inference
-
Other unnamed rules
- proof by contradiction
- informal "Rule of Equivalence"
"Trivial" ones
- conjunction
- disjunctive syllogism
- modus tollens application
- simplification
- addition
- syllogism - 2
- syllogism of OR
- reverse syllogism of OR
- reverse syllogism of OR
-
Proof
- theorem: assuming following conditions
- wants to prove:
- process
- // premise
- // rule of equivalence
- // premise
- // rule of syllogism 2,3
- // premise
- // rule of syllogism 4,5
- above proof: can be checked by machine!
- if it understands all symbols, etc.
- 👨🏫 above: a "formal, mathematical" proof
- and, we can now add a new rule
- theorem: assuming following conditions
Predicates and Quantifiers
-
Predicates
- Boolean statement w/ variable
- : a predicate if it becomes a prop. when is replaced by a value
- 👨🏫in our UNIVERSE
- : a predicate if it becomes a prop. when is replaced by a value
- examples
- // false
- // true
- however, if if out "universe" is that of integer
- no solution for the above exists
- we can have multiple variables, too
- Boolean statement w/ variable
-
Quantifiers
- universal quantifier
- "forall (in universe) s.t. "
- existential quantifier
- "exists (at least one in the universe...) s.t. "
- example:
- if universe is within the : true
- alternatively:
- universal quantifier
-
Rules on
- relation
- ⭐distributive law
- 👨🏫 but not the following!!
- there can be a that satisfies "either" one, but not both
- e.g.
- one on the left: w/ stricter requirement
- also: following is wrong, for the same reason
- there can be a that only satisfies one predicate
- e.g.
- one on the left: w/ looser requirement here
- relation
Defining Natural Numbers
-
Natural numbers
- highschool definition:
- 👨🏫 not good! vague, what does the mean?
- solved by Peano, in 19th century
- Peano axioms
- 0 is a natural number
- rules below: exists as equality wasn't defined by then...
- for every natural number ,
- ...
- every natural number has a successor
-
- i.e. is a one-to-one
- if is a set s.t.
- ⭐then
- 👨🏫 basis of all mathematical induction
- 0 is a natural number
- example: I want to prove
- let be the set of all natural no. s.t.
- showing two things are sufficient:
- holds
- highschool definition:
COMP 2711H: Lecture 3
Date: 2024-09-03 23:47:29
Reviewed:
Topic / Chapter: Induction, Well-ordering and Infinite Descent
summary
❓Questions
Notes
Proof from Peano Axiom
-
Definition of +
- definition will be recursive
- define some terms
- ...
- rules
-
- addition of 0 (identity)
-
- addition of a number, that is successor of something else
-
-
Prove
1+1=2 -
Prove
2+2=42+2=4means- furthermore:
-
Definition of
- rules
- 👨🏫 can you define division?
- rules
-
Mathematical induction
- to show holds
- it is sufficient to show
- holds
- aka: induction base
-
- inductive step
- holds
-
Definition of
- 👨🏫 other, better definitions exist!
-
Problems
- prove that
- inductive base
- inductive step
Well-Ordering Principle
-
Well-ordering principle
- every non-empty subset A contains a least / smallest element
- alternatively: set of is "well-ordered" by its natural / magnitude order
- i.e. in order
- : can be 0
- i.e. in order
- principle: mostly driven from mathematical induction
- taken as granted from Peano axioms
- : the smallest inductive set
- one can show: set of all natural no. s.t. " is well-ordered" is inductive
- and therefore must contain all natural no.
- 👨🎓 ~= reverse direction of mathematical induction?
-
Proof by infinite descent
- aka Fermat's method of descent
- you can't have an infinite sequence of s.t.
- particular kind of "proof by contradiction"
- showing: if the statement was to hold a number
- => it can hold a smaller number
- => has lower bound (0); thus it's wrong
- relies on the well-ordering principle
- often used to show that no solution exists
Proof Examples
-
Problem 2: proof on irrationality of
- theorem:
- let and
- i.e. is even => is also even
- thus
- a ever-smaller fraction can be found, infinitely!
- which is impossible, or is a "contradiction"
- i.e. no such integer exists!
- 👨🏫 also, keep in mind:
-
Proof in well-ordering principle
- let
- proof by contradiction
- step
- if is not empty, there must be smallest set from
- let be smallest number from
- however: we can obtain a even smaller member based on
- thus: it must be the case that is empty
- if is not empty, there must be smallest set from
-
Proving: "There are infinitely many prime numbers"
- let be all the primes
- if is prime: premise is wrong as is not in the list
- if
- it must be the case that is a prime that's not on the list
- (contradiction)
- or: can be factorized to
- it must be the case that is a prime that's not on the list
- and so on,
- and
- however: the sequence must be finite (infinite descent)
- and the last element of the sequence, must be a prime
- that is not on the list!
- q.e.d.
-
Problem 4 (Pigeonhole principle)
- if we have holes and pigeons are put in them
- a hole w/ at least two pigeons
- (for )
- proof by induction
- base case: starts from
- there is only 1 hole, with 2 pigeons
- so there is a hole w/ 2 pigeons
- induction step:
- for -th hole, you can either put
- 2 pigeons: problem solved
- 1 pigeon: , which is premise
- 0 pigeon: is sufficient as there are more than pigeons already
- for -th hole, you can either put
- base case: starts from
- if we have holes and pigeons are put in them
-
False proof: all cars are the same color
- base case: when , cars have the same color!
- induction step
- first cars have the same color
- and last cars have the same color too
- 👨🏫 yeah, all crs have the same color!
- it's wrong when !
- and you can't prove that
-
False proof: all man are bald
- base case: if you have 0 threads of hair, you are bald!
- inductive case: if a man with threads of hair is bald, having threads doesn't really make you not bald either!
- thus, all man (unless they have negative or fractional hair) are bald!
-
Problem 5: players take part in a tournament
- every player plays against every other player
- and every game has one winner
- prove that there exists a permutation
- s.t. has lost to
- proof
- when , the case holds
- if we can sort for players
- for , has it won over ?
- if so, we can place it after
- if there was no place to put , it shows that it has won against no one
- in which, we can put in the first place
- for , has it won over ?
- every player plays against every other player
-
Proving induction is valid
- roadmap
- show infinite descent well ordering (1)
- show induction holds from well-ordering
- let be a non-empty set w/o a smallest element
- pick any
- and : must be another non-empty set w/o a smallest element
- and smaller than
- else: proof ends
- pick any
- and : must be another non-empty set w/o a smallest element
- and smaller than // infinite descent!
- thus: based on infinite descent principle, well ordering holds
- let be a set of all of natural number s.t.
- i.e. trying to prove the fifth Peano axiom
- proving: ; suppose (contradiction)
- // A: non-empty (by definition)
- let be the smallest element of
- is not in
- thus, is also not in
- however, is smaller than , and it also shouldn't be in either!
- roadmap
COMP 2711H: Lecture 4
Date: 2024-09-09 02:14:53
Reviewed:
Topic / Chapter: Infinite Descent and more PProofs
summary
❓Questions
Notes
Infinite Descent (cont.)
-
Relationship between three
- infinite descent: implies well-ordering
- well-ordering: implies induction
- 👨🏫 can we assume the reverse?
-
Well-ordering: implies infinite descent
- let be an infinite seq. of numbers
- then
- has a minimum
- as is non-empty
- and
- then cannot be smaller than
- as is the minimum
- thus, there can't be an infinite sequence of that is always decreasing
-
Induction: implies well-ordering
- let
- and does not have minimum (proof by contradiction)
- to be proven by induction
- : for ,
- unless: is the minimum element in
- and it cannot be in
- unless: 0 becomes the min. element of
- assuming ,
- suppose
- which means:
- however, all elements is not in
- becomes the minimum element in !
- thus: the inductive assumption is wrong: and
- finally,
- i.e.
- contradicts our initial assumption: being non-empty
- thus, every non-empty subset of has a minimum element
- : for ,
Fibonacci Numbers
-
Fibonacci numbers
- e.g.
Problems
-
Problem 1
- base cases
- prove
-
Problem 2
- base case:
- then:
-
Problem 3
- 👨🏫 simply subtract the result of (2) from result of (1)
-
Problem 4
-
- i.e.
- or: they are relatively prime
- with well-ordering & infinite descent
-
- to be proven:
- proof by contradiction: assume
- let be the smallest element of
-
- i.e. divides both
- and
- if
- then also
- however: is supposed to be the "smallest element" in
- thus: contradiction, and is empty
- or: using infinite descent
- (continued from above) ...
- infinite sequence & decreasing -> impossible!
- also: using induction
- base case holds:
- induction:
- proof by contradiction
- (hopefully )
- i.e. divides both
- then for , also
- but, as
- 👨🏫 any of three will work, but just that one will be more human-intuitive!
-
-
Problem 5:
- by induction, so base case:
- assume , then:
-
Problem 6
- let , then has subsets
- base case: , then has only 1 subset:
- , so it holds
- proof by induction
- let be a set of size
- any s.t. is of size too
- then, has two groups of subsets, one including and those that are not
- each of size
- together: of size
-
Problem 7
- let be a non-empty finite set
- let
- let
- prove that
- base case:
- let be a set of size
- let with
- let
- subsets without :
- odd:
- even:
- subsets with :
- odd:
- even:
- and
-
Problem 8
- suppose: we have a class of students
- let
- in how many ways can we choose and ?
- 👨🏫
- if
- if
- 3 choices
- if
- 9 choices (as grade of a student is independent of another)
- assume: for , there are ways
- induction
- there are ways to allocate first students
- and 3 ways to allocate the last student
- as they are independent (in this course), there are ways
-
Problem 9
- reducing game / game of Nim with two heaps
- given
- players, in turn, choose either and decreases it
- if one can't make move: then the player loses
- assuming ideal play
- if then player 2 wins
- if then player 1 wins
- and assume as the order doesn't matter
- base case:
- player 2 wins
- using induction on
- with
- if player 1 reduces to
- player 2 can also make to
- strong induction
- proving
- consists of:
- holds
-
- i.e. more stuff & requirements
- prove that player 2 wins
- , player 2 wins
- player 2: can copy player 1's move
- i.e. player 2 makes equal
- can also be proven with infinite descent
- game: ends at some point (i.e. when )
- and player 2 wins it
COMP 2711H: Lecture 5
Date: 2024-09-09 17:57:10
Reviewed:
Topic / Chapter: Practice Problems
summary
❓Questions
Notes
Even More Problems
-
Problem 1
- prison guard
- prisoner gets to assigned a number ()
- they know what number they were assigned
- and
- can say: 1 sentence, only once
- "I know out number and it's (n,m)"
- show that: they will be able to come to an answer
- :
- base case:
- one with 0 can immediately shout out
- solved on day 1
- base case:
- if either number was 0, the prisoner would have said
- however, if no one shouted it on day 1, prisoner w/ no. 1 can know that his/her number is the min. and the other no. is
- solved on day 2
- : if , then it will be announced on day
-
- as, if it was , then it would have been announced on day
- it wasn't the case, so the prisoner with can announce on day
-
Problem 1'
- a prisoner: supposed to be executed
- someday next week, but not known
- 👨🏫 and you will be surprised
- prisoner: cannot be executed on Sunday
- as he won't be surprised on that day
- prisoner: cannot be executed on Saturday
- as he won't be surprised to be so by the end of Friday
- and so on...
- prisoner: I ought not to be executed!
- answer: he was executed on Wednesday, and he was surprised
-
Problem 2
- 2d lattice: all points of form where
- for each point: has natural number written on it
- number written on point: will be mean of its neighbors
- neighbor: i.e. on m
- prover all the number are equal
- proof by well ordering
- all numbers assigned to points
- has a minimum value
- and the minimum value's neighbors: must all be
- unless: there must be a neighbor that is bigger than
- then there also must be a neighbor with natural number smaller than , too
- all numbers assigned to points
-
Problem 3
- there is a circle w/ circumference 1
- and there are cars on its circumference
- and each can go distance , and fuel can be shared
- if , there exists a car that can catch & steal others' fuel, and make a full round
- base case:
- with only 1 car, w/ , then the car can make a whole round
- or:
- induction case:
- : denotes distance till the next car
- there exists at least 1, "good" car that can catch another car ()
- however, it doesn't mean that the car can make a whole round after the catch
- 👨🏫 idea: removing the "good" car, and making it with cars only
- remove the good car , and eliminate
- and change fuel of car to
- intuition: if a car could reach car , then it can reach car with this wormhole & fuel change
- 👨🎓 it is, kind of equivalent, considering car is a "good" car
- and, still, this subproblem w/ cars: satisfy
- ⭐👨🏫 we don't get to choose the instance of cars, as we must show it holds for all combinations
- however, we can do so for cars, as it is the assumption we are having
-
Problem 4
- there are no four positive integers s.t.
- proof by contradiction
- assume: assignment s.t. making minimum exists
-
- RHS: multiple of 3
- LHS: must also be multiple of 3
- and sum of two such numbers: must be within
- and only occurs when both numbers are multiple of 3
- if
- if
- and : smaller then , clearly
- contradiction: thus no such solution exists
- assume: assignment s.t. making minimum exists
- there are no four positive integers s.t.
-
Problem 5
- graph problem: a country w/ cities
- and exactly 1 road between any two cities
- and all are 1-way
- a city : a central city
- if every other city can reach directly / or with 1 stop
- show that there exists at least 1 central city
- proof by induction
- : it works
- for city: all other cities will have road to
- or other city that has road to
- by adding a new city
- if has road to : remains the central
- if has road to :
- if has any road to 's first neighbor: remains the central
- else:
- and first neighbors of : has direct road to
- second neighbors of : can access through first neighbors
- is the new central
- extremal proof
- count: how many roads are coming in
- such count:
- i.e.
indegree
- if : a city w/ maximal indegree
- then is the capital
- proof
- there are first neighbor cities of
- and other cities
- if it has road to first neighbors: can access in two steps
- doesn't make not-a-capital
- if it has road to first neighbors: can access in two steps
- is not capital only when:
- and all first neighbors are towards a different city
- 👨🎓 as: if that city had road towards any of first neighbors / , it can reach easily
- must be the other direction
- i.e. if had indegree, new city has at least indegree
- 👨🎓 as: if that city had road towards any of first neighbors / , it can reach easily
- however, it's a contradiction in choice of
- as is supposed to be a city w/ maximal indegree
- and all first neighbors are towards a different city
- count: how many roads are coming in
COMP 2711H: Lecture 6
Date: 2024-09-11 04:36:04
Reviewed:
Topic / Chapter: Counting
summary
❓Questions
Notes
Counting
-
Counting
- how many ways is there to do something?
-
PA: principle of addition
- there are 2 points,
- there exists 2 roads, 2 ferry routes, and 1 flight route
- how many ways?
- i.e. dividing big set's size into sum of smaller sets' size
- there are 2 points,
-
PM: principle of multiplication
- when noe event is independent of another
- same city
- but intermediate also exists
- a-c-d-b in linear order
- a-c: 2; c-d: 3; d-b: 2 ways
- total ways of a-b, without going back:
- ways
- as long as no. of later choices (not individual cases of later choices) are independent of previous choices, we can simply multiply
- another way to divide a large set
-
Counting permutations
- prof's notation:
- permutations of :
- 6 ways!
- how many permutation for numbers?
- e.g. how many different (linear) queues?
- use notation to denote permutation ways of
-
- i.e. inserting -th person into queue of people
- slots to insert!
- definition: can be either multiplication / permutation of
- as there is 1 way of aligning 10 people
- e.g. how many different (linear) queues?
- or, different approach:
- for objects
- how many choices do I have for 1st place?:
- how many choices do I have for 2nd place?:
- ...
- how many choices do I have for last place?:
- total:
- 👨🏫 note that no. of later choices are independent of previous choices
- for objects
-
Permutations
- how many queue of length can we form from people?
- or:
- 👨🏫: double counting: we consider and as different queue
- order matters here!
- or, think of other way
- it's still -length queue, but the last elements do not matter
- thus:
- it's still -length queue, but the last elements do not matter
- how many queue of length can we form from people?
-
Permutations of non-distinct items
- how many permutations does each word have
- not necessarily meaningful
- : all letters are distinct
- ways to order
- simple:
- there are ways to simply display
- if it was
- but order of 2 As and 2 Bs doesn't matter
- so ways of double count
- distinct ways
- there are ways to simply display
- : some letters appear more than once!
- 5 A, 2 B, 2 R, 1 C, 1 D
- all permutations:
- general way
- there are alphabets in a word
- where each letter appears times
- total no. of permutations:
- one of the ways we show that a fraction is an integer
- claim that it is answer to some counting problem
- all counting problem: has integer solution
- claim that it is answer to some counting problem
- 👨🏫 I'll fail you if you say there are 9.5 ways of counting!!!
- how many permutations does each word have
-
Combinations
- 👨🏫 what if we don't care about the order?
- e.g. how many subsets of have size
- notation:
- equivalent: how many binary seq. of length have ones?
- or, a different way
- : no. of different permutation of length from
- then divide it by : no. of different ordering of length
- thus:
- : no. of different permutation of length from
- 👨🏫 what if we don't care about the order?
Practice Problems (Permutations)
-
Idea
- has subsets
- old method we used:
- : false; : true
- and we can assign for each elements
- to assign: whether it's included in subset / not
- or, using counting:
- there are 2 choices for first element
- and so on for all elements, independent of previous choices
- thus ways total
-
Problem 1
- how many subsets are there of , including no. ?
- consider: first element must be 1
- only single way for first element
- for the rest elements: ways
- how many subsets are there of , including no. ?
-
Problem 2
- how many no. of subsets of even size?
- answer: ways
- 👨🏫 it doesn't apply for (not natural number)
- if
- how many seq. have no 1s (= true)?
- way:
- how many seq.. have exactly 2 1s?
- i.e. different permutation of word:
- how many seq. have exactly 4 1s?
- (same combination, just 0s and 1s in worst change)
- how many seq. have exactly 6 1s?
- way:
- answer: sum of all
- answer: ways
- how many no. of subsets of even size?
-
Problem 3
- how about for general ? (PA)
- i.e. how many seq. of length have ones?
- ones, zeros
- total sum:
- 👨🏫 more complicated than thought :p
- can we show that those two are same?
- e.g. using induction, etc.
- i.e. how many seq. of length have ones?
- how about for general ? (PA)
-
Problem 4
- for general (PM)
- how many ways to assign fill in to elements
- for first elements: we have freedom of choice
- for the last element: we can only make choice
- dependent on others
- thus,
- how many ways to assign fill in to elements
- for general (PM)
Practice Problems (Combination)
-
Problem 5
- prove
- 👨🏫 disclaimer: I don't expect you to be able to do any algebra
- it's just different way of counting all subsets, so
- prove
-
Problem 6
- prove
- as there is a pair for each size
- 👨🏫 same number of even & odd subsets!
- prove
-
Problem 7
- prove
- show it in combinatorial proof
- recruiting captain & team, total of people, from
- choosing 1 captain from people & choosing the rest from people
- = choosing people from people & choosing a captain from people
-
Problem 8
- prove
- somewhat the same
- no. of all teams
- = no. of teams excluding a person A + no. of teams including a person A
-
Problem 9
- prove
- RHS: 3 possibilities for a person
- and all possible subsets
- LHS: for all group, where
- people are in group
- and people are in group
- also:
- among people, there are total of ways to divide them between group
- thus same
-
Problem 10
- how many solutions does
- have if ?
- if : 1 solution
- if : w/ unique value
- what if ?
- 👨🏫 can we reduce the problem into permutation / combinations?
- e.g. same as dividing balls with 2 bars
- w/ 11 slots
- or: aligning 10 balls and 2 bars
- and the 10 balls & 2 bars are indistinguishable within them
- for general problem,
- where
- there are
- as we have bars
- or, the other way:
- choosing slots for bars from slots
- i.e.
- how many solutions does
-
Problem 11
- prove
- where
- choosing people from people:
- same as choosing people from whom you will exclude
COMP 2711H: Lecture 7
Date: 2024-09-16 02:53:37
Reviewed: 2024-10-07 02:47:38
Topic / Chapter: More Counting Problems
summary
❓Questions
Notes
Arrangement Along the Circle
-
Problem 1
- how many ways can people sit around a circle?
- rotation / shifting of an arrangement: is considered equivalent / same permutation
-
Problem 2
- how many ways cab we put distinct people around identical circles?
- i.e. no. of tables
- assume: ?
- find relation using induction-like approach
- 👨🏫 let's notate the solution as
- base case:
- person is either
- in a circle on their own:
- as we need to place the rest
- sharing a circle
- how many ways can we insert?
- at least ways, as there are tables
- as there are people already on the table, and we are choosing, "who is on the left?"
- in a circle on their own:
- how many ways cab we put distinct people around identical circles?
-
Problem 3
- in how many ways can we people around circle if 2 people must not be next to each other?
- as there are ways of ordering people around the table.
- 👨🏫 or:
- no. of ways to put them together(when ),
- and there are total permutation
- thus
-
Problem 4
- how many ways cab we put distinct people around identical circles?
- if 2 people must not be next to each other?
- case: no. of ways to put two people together
- case 1: setting up a new table for them
- case 2: sharing table w/ people
- case 1: setting up a new table for them
- finally:
- (and subtracted from all no. of permutations)
- ❓ can't we simply treat two people as one?
- i.e.
- how many ways cab we put distinct people around identical circles?
-
Problem 5
- let be a set of elements
- what is the no. of pairings in
- 👨🏫
- and no element can be pair of itself
- solution 1
- steps
- after choosing an element, there are ways to choose its pair
- after choosing the next element, there are ways to choose its pair
- ...
- after choosing the penultimate element, there are 1 way to choose its pair
- i.e.
- steps
- solution 2
- simply showing all linear permutations
- and grouping them together
- there are ways to ordering the elements
- and ways to order different groups and ways to order groups within it
- thus
- solution 3
- if order is accounted:
- and there are different ways to order them
- thus,
- if order is accounted:
- let be a set of elements
Weekly Problems
-
Problem 1: Week 2
- how many permutations of people satisfy ?
- 👨🏫 aka: derangement
- show recursive solution
- let no. of ways to arrange w/ people / elements
- (similar logic as then )
- general cases
- person sits on chair
- two cases
- sits on chair ()
- does not sit on chair
- as: each people (except ): has exactly ine forbidden sit
- for :
- for : (as that is the condition)
- so: it's a direct subproblem of size
- solution:
- i.e. no. of choosing , then recurrence holds for each cases
-
Problem 5: Week 2
- 73 boys, 9 girls; 82 total
- how many permutations s.t. all girls appear before all boys?
- part 2: having 7 girls in top half, and 2 girls in bottom half
- top half: 7 girls & 34 boys
- bottom half: 2 girls & 39 boys
- one of the solution:
- choose who will go in the top half
- (no need to choose who will go in the bottom, as those are complements from top half)
- choose who will go in the top half
- part 3: no two girls are next to each other
- detour:
- no. of solutions of ;
- consider: 10 blocks, separated by 2 (=3-1) bars
- there are 11 slots total
- so
- no. of solutions of ;
- let
- then the same condition!
- thus:
- similarly: consider girls as blocks, and boys as bars
- first, there are ways to order the girls
- and let no. of boys after girl (and : no. of boys before girl 1)
- ;
- let:
- and for all others:
- now we have
- thus:
- however, boys (nor girls) are considered distinct
- so:
- detour:
- and with permutations:
- part 4: no three girls are next to each other
- one solution: adding constraints, such as:
- let : no. of solutions for the question
- solution: either starts w/ boy or a girl
- case 1: seq. starts w/ a boy
- as any boy can be the first
- case 2: seq. starts w/ exactly one girl?
- ways to choose
- case 3: seq. starts w/ exactly two girls?
- case 1: seq. starts w/ a boy
- 👨🎓 how about the base case..?
-
Problem 6
- how many rectangles are there?
- i.e.
- and
- finally:
-
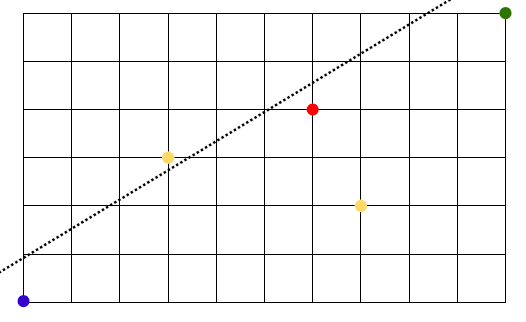
Problem 7
- how many ways are there of moving, from blue to green?
- 👨🏫 you can only move up & right
- so there are 16 possible moves, 10 being
Rand 6 beingU - thus:
COMP 2711H: Lecture 8
Date: 2024-09-16 17:59:47
Reviewed: 2024-10-07 02:49:12
Topic / Chapter:
summary
❓Questions
Notes
Revisiting Problem
-
Problem 2
- how many ways can we put distinct people around identical circles, while ensuring 1 and 2 are next to each other
- simply: glue 2 people together
- thus , and times 2 as you can order between two people can swapped
- however: if there is a circle w/ two people only:
- ordering doesn't matter
- i.e. cases are counted twice
- however: if there is a circle w/ two people only:
- finally:
- then subtract it from the real, total, number to find how many ways aan we allocate people while separating the two
-
Weekly Problem 5
- ways of ordering boys
- are there are 74 slots we can insert girls
- and at most 1 girls can be inserted / slot
- i.e.
- however, as order of girls matter too, so
- 👨🏫 this leads to new method of solving the equation!
- if
- i.e. if we have constraint:
- then we only have only 6 slots (7-1) to insert 3 bars (4-1)
- part 4: we cannot have 3 consecutive girls
- 👨🏫 casework: better done on girls, as we have much less girls than boys
- girls: divided into conseq. groups of 1/2 (not 3)
- 👨🎓 ~= counting problem? how many ways to pay 9 dollar w/ 1 dollar and 2 dollar banknotes? orders matter
- 👨🏫
- no. of ways to write as sum of summands of 1 or 2
- 👨🎓 summand: operand of summation
- if last summand is :
- if last summand is :
- thus
- thus: total of ways on grouping & ordering girls are as of following
- for min. groups of girls; for max.
- back to boys, we have slots to put boys
- and let's denote the no. solution as
- 👨🎓 bars w/ balls
- for real, finally:
- as all boys are distinct as well
- computable by hand (unlike previous recursion)
- computing better:
- coins, with 2-coins and 1-coins
-
Weekly problem 7
- 10 R's and 6 U's, can be presented as
-
- aka
- or, the other way:
- aka
-
Weekly problem 8
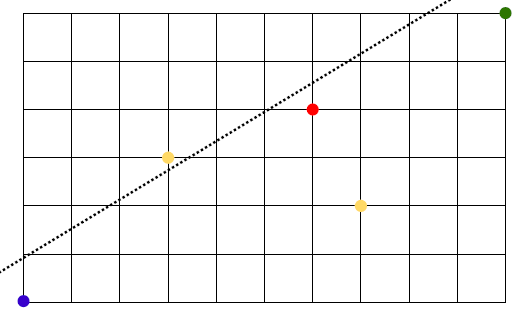
- how many no. of ways from blue to red does NOT go through red point?
- total ways:
- total ways B->R:
- total ways R->G:
- finally:
-
Weekly problem 9
- how many no. of ways from blue to red does NOT go through yellow point?
- however: no path can go through both yellow points!
-
Weekly problem 10
- how many paths do we have that do not cross the dotted line?
- like Pascal's triangle, or Fibonacci numbers, you can simply add up paths from two points together!
-
Problem 8 from 102 problems
- Spider with 8 legs
- w/ 8 socks () and 8 shoes ()
- and how many permutations are there, that spider wears before corresponding ?
- first, there are ways
- however, there is a double counting per each leg, correct order & incorrect order
- thus,
- instead, it's like a sequence of size 16 s.t. each number 1-8 appears exactly twice
- count the first one as socks, second as shoes
- finally, 16 numbers with 8 groups of 2 indistinct numbers
- so
-
Divisors
- how many divisors does 640 have?
- 16 divisors! as all its divisor will look like
- where
- how many common divisors do 100 and 640 have?
- and all common divisor: in
- s.t
- i.e. min appearing size of either
- ways
- 👨🏫 also,
- and all divisor of : common divisor of both numbers
COMP 2711H: Lecture 9
Date: 2024-09-23 09:11:39
Reviewed: 2024-10-07 03:13:46
Topic / Chapter: Principle of Inclusion & Exclusion
summary
❓Questions
Notes
Functions
-
Derangements
- for , how many s.t.
-
- choose first, then do casework
- what if: exactly people, among , must be in position?
- how many such exist?
- or: exactly position s.t.
-
- i.e. deranging people
- and choosing people to remain seated (in their own)
- and for remaining people: only one way
- i.e. deranging people
-
No. of functions
- how many functions from to are onto?
- or: surjective (French)
- i.e. all elements of has mapping?
- first, how many functions w/ possible input and possible output exist?
- if , there is only 1
- if , there are
- and subtract no. of non-onto functions
- i.e. all mapped to , or only
- = 2 cases
- onto functions
- how about a recursive formula?
- first: choices for input , let's say was chosen
- then, later ones: can either include or not
- or: consider the reverse mapping. What's mapped to ?
- i.e. subset of mapped to
- assume: inputs are mapped to
- i.e. possibilities
- first: choices for input , let's say was chosen
- also: it's the same as dividing into non-empty sets
- based of the output they are mapped to
- let : no. of ways of dividing into non-empty sets
- without order
- 👨🏫 same as the ball-and-box problem!
- if the ball is in its own box:
- if the ball is sharing its bow with others
- how many functions from to are onto?
-
Problem 1: how many paths do not go through marked segments?
- i.e. segment ,,,
- let : no. of paths to point
- but, how many (invalid) paths go through at most exactly segments?
- simply: count each cases manually
- going through and
- 👨🏫 is there a more elegant formula?
- : no. of paths to point , including exact paths
Principle of Inclusion & Exclusion (PIE)
-
Principles of inclusion & exclusion
- how many no. are divisible by ?
- how many no. are divisible by ?
- how many no. are divisible by both ?
- i.e. multiple of
- how many no. are divisible by ?
- no double counting!
- same as:
- how many no. are divisible by ?
- same as:
- i.e. eliminate double counting within double-counted elements!
- ()
- same as:
- how many no. are divisible by ?
- same as:
- i.e. eliminate double counting within double-counted elements!
- ()
- same as:
- how about sets?
- finding the pattern
- let
- then
- 👨🏫 how can we prove it without induction?
- induction: painful...
- proof: let , suppose is in exactly sets
- 👨🏫: ensure you count only once for both sides!
- if : it only gets added once in
- if : it only gets counted once in
- for general : gets added
- no. of being added: in , in
- 👨🏫 as proven, there are equal no. of even subsets & odd subsets (including )
- but we don't have in out equation (which could have been subtracted)
- thus,
- from
- how many no. are divisible by ?
-
Problem 2: derangements
- how many permutations of exist s.t. ?
- : set of perms s.t.
- solution:
- not in position for all
- and, as we have total perms
-
- as there are permutations
- (as there are )
-
- to be subtracted
- as converges to infinity, probability of picking a derangement:
-
- : used because exponent of inside sum changed
- according to PIE
-
Problem 3: how many functions from to are onto?
- i.e. all element w/ at least 1 mapping?
- let : set of functions not covering
- let : set of functions not covering
-
- 👨🏫 we can do so because we know that size of are all same
- ... and so on; thus:
- and, as above is the set of non-onto function
COMP 2711H: Lecture 10
Date: 2024-09-23 17:44:16
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Problems
-
Paths excluding forbidden segments
- w/ PIE, instead of addition principle
- idea: get all paths, subtract paths going through one forbidden, add paths - thrice, .. add -th and so one.
- how many paths go through exactly 3 forbidden segments?
- from generalized PIE:
- all path going through forbidden - all path going through forbidden, so on.
- or:
- (for our case)
- from generalized PIE:
-
No. of primes below 50
-
- i.e. at least one factor: less than
- primes less than :
- only needed number for composite no. below 50
- : mults. of 2 (and so on for )
-
- i.e. no. of composite numbers below
- all no. of primes:
- 👨🏫 maybe better
- but I, as a CS people, hate any algorithm w/ PIE (unless it's optimal)
-
-
Integer solutions w/ more bound
-
- how many solutions satisfy exactly two of the upper bounds?
- : solutions violating
- :
- :
- total no. of solutions:
- no such solution satisfying more than 1 red bounds
- e.g. :
-
-
Generalized PIE
- universe w/ elements
- : sets
- : no. of elements appearing in exactly of the sets ()
- let element : appears in sets
- must be counted only once on the left hand
- appearing in sets
- thus
- what if appears in sets?
- and
- thus
- therefore we must add on RHS
- for with
- sub
- universe w/ elements
-
r-permutations of : exactly fixed points?
- fixed point of : index s.t.
-
- set of all s.t.
- set of all s.t.
- set of all s.t.
- set of all s.t.
-
- chairs: left
- and people left
- ⭐ solution:
-
- exactly people in correct position
-
- 👨🏫 extended version!
COMP 2711H: Lecture 11
Date: 2024-09-25 09:07:42
Reviewed: 2024-10-07 04:09:42
Topic / Chapter: Pigeonhole Principle
summary
❓Questions
Notes
Pigeonhole Principle
Problems
-
Problem 1: Squares
- squares
-
Problem 2: Handshake
- people: attend party
- some: shake hands
- let : no. of handshake person has made
- show: (even)
- trivial as there always exist
- show: there are two people
-
- different holes, for people
- however, we can
- case 1:
- i.e. for every
- as one person didn't shook hands with anyone
- with people left: there exists at least one hole with 2 or more people
- as there is a person in hole in the first place
- case 2:
- i.e. for every
- hole for people: must be double count!
-
-
Problem 3
- show that:
- let
-
- infinite set!
- actually: you can have of them
- but, as it's infinite set, there are infinite such solutions
- infinite set!
-
- there must be at least 1 collision in numbers
- then:
- 👨🏫 size of : doesn't matter
- show that:
-
Problem 4
- show that
- grid,
- goal: to make every row, column, and diagonal: has different sum
- is this doable?
- there are possible sum:
- but there are 8 numbers: for row, column, and diagonal
- thus, there must be at least one collision
- show that
-
Problem 5
- for a set of integers
- attempt 1
- subsets of
- : (non-empty)
- :
- while it shows: there exists a collision
- doesn't show that
- also, if
- and
- then : solution to this problem
- attempt 2
- enumerating:
- i.e.
- when
- there are two subsets
- s.t.
- then,
- however: works only if empty set is included
- not considering an empty set:
- for a set of integers
-
Problem 6
- problem
- let ;
- show that there are two disjoint non-empty proper subsets of
- w/ the same sum
- rules
- how many proper subsets:
- i.e.: we have 1022 pigeons
- and there must be at least 2 non-empty proper subsets w/ same sum
- as
- disjoint part:
- if
- then
- as you can subtract the same number
- if
- problem
-
Problem 7
- 15 people w/ 100 coins in total;
- show: two of them have the same number of coins
- if each person has different no. of coins:
- thus min:
- two: forced to have the same no. of coins
- 15 people w/ 100 coins in total;
-
Problem 8
- football team w/ 20 games
- scores in all of them
- team: scores goals in total
- show: there is a sequence of conseq. games s.t. the team has scored:
- exactly 9 goals
- 👨🏫 problem w/ bunch of numbers: either induction / pigeon hole
- : no. of goals in -th game
- ;
- 30 different values:
- prove: s.t.
- and all : distinct as
- for all
- and all : distinct as
- let's try to avoid having difference
- intuition: for each choice, you lose at least 1 choice
- e.g. if you choose , then you can't choose
- alternatively: you can "pair" numbers up s.t.
- you can choose at most one number from them
- e.g. and
- intuition: for each choice, you lose at least 1 choice
- 👨🏫 is there a more elegant way?
- let , another
- , another
- , another
- ...
- , another
- there are 40 numbers on left & right combined
- where we have 30 possibilities
- however: we must choose those two numbers from different sides
- let , another
- football team w/ 20 games
-
Problem 9
- let and
- prove that there exists four different no. s.t.
- s.t.
- alternatively:
- 👨🏫 preferable as subtraction has less variety than addition
- , so there are pairs
- if
- we have:
- so there exists at least two pairs:
- s.t. their difference: same
- as
- yet, we want for distinct numbers
- while can be true
- then, we can eliminate pairs with duplicated value
- if , then we can eliminate either
- or
- but if at the same time
- thus solution discovered
- if , then we can eliminate either
- prove that there exists four different no. s.t.
- let and
-
Problem 10
- 6 candidates for president
- every pair of candidates: either friends or enemies
- show, there are 3 candidates friend to each other
- or enemy with each other
- 👨🏫 can be represented as a graph, with edge being different color
- statement claims: there exists at least 1 all-blue or all-red triangle
- choose 1 candidate
- 6 candidates for president
-
Problem 10+
- IMO 1964
- 17 people correspond: by mail with each other: one with all the rest
- only three topics are discussed
- each pair of correspondents: deal with 1 of these topics
- prove: that there are at least tree people, writing to each other, about the same topic
- choose 1 candidate
- among mails, at least should have the same topic
- a
- what if: four different..?
- 17 people correspond: by mail with each other: one with all the rest
- also: HW
- IMO 1964
COMP 2711H: Lecture 12
Date: 2024-09-30 09:04:41
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Graph Theory
-
Graph Theory
- 👨🏫 geometry: doesn't matter:
- only thing matters: whether edge / path from point to exists
- e.g. can send message to ?
- graph :
- tuple of vertices & edge
- : set of vertices
- mostly: are finite (sometimes not)
- : a finite set of edges
- every : of form
- two graphs with same : equivalent
- i.e. we on't care about
- loop: an edge
- i.e. edge where start = end
- 👨🏫 stupid idea if you think of it as computer network
- simple graph: graph without loop
- if : : neighbors / adjacent
- complete graph: when every element is neighbor of every other one
- complement: empty graph
- : complete graph on vertices
- complement:
- 👨🏫 geometry: doesn't matter:
---
title: G
---
graph LR
1((1))
2((2))
3((3))
4((4))
1<-->2
1<-->3
1<--/-->4
2<-->3
2<--/-->4
3<-->4
---
title: G'
---
graph LR
1((1))
2((2))
3((3))
4((4))
1<--/-->2
1<--/-->3
1<-->4
2<--/-->3
2<-->4
3<--/-->4
- : has vertices
- : subgraph of if:
-
Isomorphism
- labels on vertices: somewhat meaningless
- 👨🎓 : as they are just names
- isomorphism: when you can re-label one graph to show another
- rigorously: for ,
- isomorphism:
- s.t. : one-to-one & onto
- isomorphism:
- degree of :
- i.e. count of neighbors
- if : is isolated verted
- theorem:
- basically: the idea of shake-hands
- say, we add edges from
- when you add ,
- adjacent matrix
- matrix where
- for simple graph: all
- as no loop exists
- if: we want to find all neighbors-of-neighbors:
- can be given by:
- 👨🏫 can be further expanded to multiple networks
- will be used more often in 3711
- walk: seq. of vertices & edges
- s.t. every
- for simple graph: it doesn't matter
- 👨🏫 however, will be useful later
- when there exists more than one edge between two vertices
- 👨🏫 however, will be useful later
- trail: walk without repeated edges
- path: work without repeated vertex
- path ⊆ trail, but not the other way
- labels on vertices: somewhat meaningless
---
title: G
---
graph LR
1((1))
2((2))
3((3))
4((4))
5((5))
1<-->2
2<-->3
1<-->3
4<-->5
5<-->3
4<-->3
- then <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">5</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">→</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0359em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>: a trail but not a path
- closed trail: when a trail begins & ends at the same edge
- aka circuit
- cycle: substitute of closed path
- and no vertices other than repeats
- and only appears in the beginning & end
- theorem: every walk: contains a path:
- weaker: if there is a walk , then also path
- proof of weaker theorem:
- consider: let : (one of) the shortest walk from
- claim: is a path
- if is not a path
- => there exists repetition of vertex
- however, then we can skip the cycle of , and go directly to
- which, provides a shorter walk
- contradiction
- proof of stronger theorem:
- can be proven w/ similar idea
-
Königsberg bridges
- exists a (multi) graph
graph LR
1((1))
2((2))
3((3))
4((4))
1<-->2
1<-->2
1<-->3
2<-->3
2<-->4
2<-->4
3<-->4
- is there a closed walk that goes through all edges exactly once?
- solved by Euler: impossible
- all the vertex: with odd number of degree
- no vertex w/ even number of degree (essential for comming-back)
-
Connectivity
- vertex connected to iff -path
- not necessarily adjacent
- a graph : connected if every pair of vertices are
- 👨🏫 internet is a connected graph
- not that they are connected in practice...
- connected component (cc): a maximal connected subset of vertices
- theorem: a graph with vertices and edges: has at least
- camps
- proof:
- empty graph w/ component
- adding an edge: decreases no. of cc at most by
- corollary: every connected graph has
- tree: connected graph with edges
- theorem: following three are equivalent
- : connected and (is a tree)
- : connected and has no cycles
- and has no cycles
- 👨🏫 like a triangle / triple iff
- proof:
- : start w/ empty graph; add edges
- at least edges must be added to make it connected
- every edge : reduced no. of cc
- however, to be a cycle: there must be an edge within cc
- i.e. not reducing no. of cc
- :
- you can't have more than edges without making a cycle
- you can't have less than edges to make it connected
- thus: it has exactly edges
- thus
- :
- you can't have more than edges without making a cycle
- you can't have less than edges to make it connected
- thus: it has exactly edges (same)
- :
- you can't have more than edges without making a cycle
- you can't have less than edges to make it connected
- thus: it has exactly edges (same)
- : start w/ empty graph; add edges
- theorem: an edge : a cut iff
- : not part of any cycle
- 👨🏫 if you forget what is iff: it's logical error
- ⚠️ leads to an F!!!
- proof: assume : a cut
- of
- s.t. removal of will make two cc disconnected
- suppose: in cycle
- if there exists a cycle: there must exist another edge connected two cc
- assume : there is an -path
- if the path doesn't include : then removal of will not diconnect the components
- if the path includes : it can still round its way through
- proof: assume is not in any cycle: prove that is a cut
- for it to not be a cut: there must exist , another path connecting components
- vertex connected to iff -path
COMP 2711H: Lecture 13
Date: 2024-09-30 18:01:10
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Trees
-
Leaves
- recall: tree = connected graph w/ edges
- leaf: a vertex of degree 1
- theorem: every tree on vertices: w/ at least 2 leaves
- proof: based on maximum path
- let : longest path
- claim: : leaves
- proof by contradiction: : not a leaf
- : cannot be connected to vertex in the same path
- as it won't be a cycle
- also: it cannot be connect to another vertex
- as it is against statement: is the longest path
- : cannot be connected to vertex in the same path
- w/ , how many graphs exist?
- 2 choices (yes / no) for total of possibilities
- or: largest set of size , and all (distinct) subset of it
- how many of above are trees?
- solution:
- translate all trees into seq. of length
- translation
- for each leaf (or: w/ min. neighbors) of tree: write its neighbor, and erase the leaf
- repeat until only one edge remains
- e.g.
graph LR
1((1))
2((2))
3((3))
4((4))
5((5))
6((6))
7((7))
3-->1
3-->5
1-->4
5-->6
5-->2
5-->7
- gets translated into `5 1 3 5 5`, vertex <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8389em;vertical-align:-0.1944em;"></span><span class="mord">5</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">7</span></span></span></span> remaining
- recovery
- if a node is originally a leaf: it won't be on a list
- i.e. 2, 4, 6
- choose a remaining one, and connect with existing node
- if a node is originally a leaf: it won't be on a list
graph LR
5((5))
7((7))
7-->5
6_2((6))
5_2((5))
7_2((7))
7_2-->5_2
6_2-->5_2
6_3((6))
5_3((5))
7_3((7))
4_3((4))
7_3-->5_3
6_3-->5_3
4_3-->5_3
6_4((6))
5_4((5))
7_4((7))
4_4((4))
2_4((2))
3_4((3))
7_4-->5_4
6_4-->5_4
4_4-->5_4
2_4-->3_4
6_5((6))
5_5((5))
7_5((7))
4_5((4))
2_5((2))
3_5((3))
1_5((1))
7_5-->5_5
6_5-->5_5
4_5-->5_5
2_5-->3_5
3_5-->1_5
- forest: graph consisted of forest
- HW: show how many forests are in all possible cases
- theorem: every connected graph w/ vertices: w/ at least non-cut vertices
- proof: w/ longest path
- even if are to be cut: its neighbors can still more
- same for
- theorem: every odd closed walk: contains an odd cycle
-
- if it is a cycle: problem solution
- or else:
- graph: gets divided into two smaller cycle, around
- and choose an odd graph, and work on it
- as it is only subgraph of original graph, its size must
- Bipartite graph:
- (disjoint)
- s.t. every edge: has endpoint in , another in
- theorem: is bipartite iff it has no odd cycles
- proof
- bipartite -> no odd cycles
- start in
- taking 1 edge: goes to opposite side
- taking odd no. of edge: goes to opposite side from starting side
- i.e. cannot form a cycle, as
- no cycles!
- no odd cycles -> bipartite
- put a vertex in
- add all its neighbor in , opposite side
- add all their neighbor in , opposite side
- ... repeat
- there can't be an edge within the same party
- as that would create an odd cycle
- bipartite -> no odd cycles
- theorem: assume a , then has a cycle
- proof
- let : a longest path
- : must be connected to somewhere
- i.e. within the path -> creating a cycle
- or: outside the path -> against the claim that is the longest path
- theorem: in finite ,
- every cc of : either a cycle or path
- pick an arbitrary
- let be entire graph
- for to create a cycle
- cannot connect to vertex in the middle:
- cannot connect to : it's a cycle
- if you stuck in a dead end: iterate through the opposite direction ()
- as the graph is finite, we can reach the end
- and apply the same rule described above
- 👨🏫 continue until this process covers your entire graph
- 👨🎓 a non-cycle non-path graph: must have at least 3 neighbors
COMP 2711H: Lecture 14
Date: 2024-10-02 01:19:04
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Graph Theory
-
Disjoint cycle
- theorem: if (connected) ,
- edge set : disjoint union of cycles
- proof: by induction
- how do we define the size of graph?
- (strong) induction on no. of edges:
- base case : works
- induction step: ,
- for a vertex in cc
- its neighbor's degree, also even
- i.e. there exists at least another path to continue
- however, it can't continue forever as 's finite
- at some point, you will
- its neighbor's degree, also even
- thus, there must be at least one cycle
- for a vertex in cc
- connected graph without cycle: tree
- but tree: at least with two leaves
- against initial assumption
- it is connected, and it shouldn't be tree -> it has a cycle
- cycle
- but tree: at least with two leaves
- after removal of all edges of
- all vertex in : loses degree of
- theorem: if (connected) ,
-
Eulerian circuit
- Eulerian circuit: closed walk passing every edge exactly once
- graph: Eulerian if it contains an Eulerian circuit
- theorem: for connected, is Eulerian iff
- Eulerian ->
- let : closed walk covering all edges once
- same vertex can appear multiple times in the middle, however
- as it enters & leaves the node, it must have even degree
- same for
- let : closed walk covering all edges once
- -> Eulerian
- let a cycle connected to multiple Eulerian circuit / graph
- staring for a vertex cycle, it can have Eulerian walk on Eulerian circuit, and come back to starting point
- 👨🏫 prove base case for yourself
- Eulerian ->
- Hamiltonian cycle: cycle visiting all vertices
- 👨🏫 solution: an NP-hard problem
- Eulerian circuit: closed walk passing every edge exactly once
-
- theorem: graph w/ edges
- w/ subgraph
- there exists a bipartite
- proof idea: consider all subgraph of
- and consider: largest bipartite subgraph
- claim:
- proof
- claim, for
- if it's not the case, then we can make largest
- contradiction: as must be the largest subgraph
- theorem:
- claim, for
- theorem: graph w/ edges
-
Graphic sequence
- given a seq.
- is the graph w/ this degree sequence?
- theorem: : degree seq of (not necessarily simple)
- iff is even
- if : trivial
- given a seq.
graph TD
a_0((a_0))
a_1((a_1))-->a_1
a_2((a_2))-->a_2
- and similarly go on
- otherwise
- no. of odd terms: must be even
- then: we can have edge between such vertex,
- and
- which is solvable by above case
- what if we want it to be a simple graph?
- seq. : graphic if a graph based on it
- Havel-Hakimi algorithm
- choose vertex w. highest degree
- theorem: a seq is graphic
- iff
- is graphic -> graphic: trivial
- graphic -> is graphic
- vertex : connected to red vertices
- yet, we want it connected to blue vertices
- then: find a vertex connected to desirable vertex
- i.e. swap neighbors, or 2-switch
- can always be found:
- they never have the same degree
- vertex : connected to red vertices
- graphic iff Havel-Hakimi algorithm works
-
Tree and unique path
- : tree iff there is a unique path between every pair od vertices
- tree: no cycle, edges, connected
- suppose : both -paths and
- implies: closed -walk -> cycle
graph LR
u((u))
v((v))
int_1(( ))
int_2(( ))
int_1-->int_2
u--π1-->int_1
int_2--π1-->v
u--π2-->int_1
int_2--π2-->v
- : has no cycles
- suppose
- thus: initial statement can be used as fourth definition of tree
-
Tree
- connected graph : tree iff all edges of : cuts
- tree -> all edge being cut
- as there is only one, unique -path, removing disconnects
- thus is a cut
- all edges being cut -> tree
- no edge appears in a cycle
- there is no cycle
- proof 2 (more independent)
- suppose : cycle in G
- then an edge in cycle: not
-
Connect
- theorem: every connected graph : w/ subgraph
- s.t. is a tree
-
- if : already a tree
- else: eliminate all edges that are not cut, one by one
- proof 2:
- choose vertex
- remove all edges except the shortest path from to all other vertex
- properties of tree
- connected
- having edges
- d
- no cycles either
- the level (distance from ): goes only up and up
- can't form a cycle
- theorem: every connected graph : w/ subgraph
COMP 2711H: Lecture 15
Date: 2024-10-07 09:06:10
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Graph Theory
-
Tree
- theorem: when edge is added to a tree , creates exactly 1 cycle
- proof
- there will be at least one cycle: as it has edges now
- there can't be two cycle: as doing so would mean following situation
- and, in this case, input contained cycle itself
graph TD
1((1))
2((2))
3((3))
4((4))
1-->2
2-->3
1-->4
1--e-->3
4-->3
- a weighted graph consists of
- : a graph
- finding: shortest path
- where distance of each edge:
- walk is more accurate, as it might not be a path
- previous theorem: every connected graph contains a subgraph
- s.t. is a tree
- such tree: spanning tree
- theorem: given a weighted graph , a subtree
- is a minimum spanning tree (MST) if it is a spanning tree w/ least total weight
- algorithm to find MST: Kruskal's algorithm
- sort: each weight in increasing order
- for each (from minimum): take the edge if it doesn't create a cycle
- 👨🏫 what is the cheapest edge to connect two connected components?
- there might be multiple MST!!
- above algorithm: finds one such MST
- 👨🏫 what is the maximum number of MST?
- algorithm works: as
- it terminates as there are finite no. of edges
- output: connected graph given input is connected
- proof: suppose the output is not connected
- i.e. there exists
- and : vertices in
- algorithm: went to all possible edges, should have checked
- let : output
- and be MST
- show:
- : sum of weights in graph (tree)
- i.e. algorithm: chooses the same edge with
- and first edge to be not in :
- consider:
- it is a cycle
- however, the output is a tree
- thus: must contain a path to connect vertices of
- let it be
- claim: is a tree
- but the method of choosing : edge w/ smallest possible weight
- thus, must have a smaller weight than
- contradiction!
- then: repeat until
- sometimes, algorithm: much simpler than proof of correctness!
- Prim's algorithm
- picks a vertex
- then pick a cheapest edge from
- let it be to
- then, pick a cheapest edge from , then repeat
- condition: not making a cycle!
- 👨🏫 what is the cheapest edge to connect an edge to my current cc?
- proof: similar to Kruskal's
- 👨🏫 hint: assume ideal path, and compare & contrast
- modify it until
-
Directed graph
- directed graph:
- where : set of vertices
- and of fork
- 👨🏫 it's not a set, thus order matters
- directed equivalent of connected component
- candidate 1:
- ignore the direction
- consider it cc if its undirected case is a cc
- 👨🏫 not very useful, as one cannot move one in cycle to another
- candidate 1:
- vertices : strongly connected (SC) iff
- both -path and -path exists
- strongly connected component (SCC): maximal subset of vertices
- s.t. every two of them are SC
- strongly connected graph: partitions your graph
- every component: SC to itself
- if SC to -> vice versa
- and ->
- transitive
- DAG: directed acyclic graph
- example
- directed graph:
graph TD
1((1))
2((2))
3((3))
1-->2
2-->3
3-->1
- : has no cycle iff: every vertex of : its own SCC
- assume: has no cycles
- let : be two vertices
- if in the same SCC: there must be both and path
- then: connection of and path: closed walk
- and all closed walk: implies existence of cycle
- 👨🏫 proof: exactly same fore directed graph
- contradiction, as is assumes to have no cycle
- thus: every vertex of : its own SCC
- without extra members
- let : be two vertices
- assume: every vertex of : its own SCC
- let : be a cycle
- if : then both and path exist
- thus, they must be in SCC
- due to assumption: each cycle: contains at most 1 vertex
- loop: meaningless
- assume: has no cycles
-
Topological ordering
- topological ordering: given directed graph
- permutation of vertices s.t. every edge : of the form
- theorem: directed graph : a DAG iff has a topological ordering
- proof
- : w/ topological ordering: implies there is no cycle:
- i.e. is a DAG
- no cycle implies topological ordering
- if there is no cycle: must exist a vertex w/ indegree 0
- unless: has a cycle
- assume: we create a left-to-right indegree
- 👨🏫 similar to prerequisite problem, ain't it
- if there is no cycle: must exist a vertex w/ indegree 0
- d
- : w/ topological ordering: implies there is no cycle:
- for directed graph, both indegree and outdegree are defined
- lemma: if a directed , if outdegree of every vertex: at least 1
- then there is a cycle
- proof: keep going until you find a previously seen vertex
- must end somewhere as the graph is finite
- similar lemma: if a directed , if indegree of every vertex: at least 1
- then there is a cycle
- proof: keep going backwards until you find a previously seen vertex
- must end somewhere as the graph is finite
- topological ordering: given directed graph
-
DAG game
- DAG game: a game w/ loopless DAG
- two players w/ starting vertex
- w/ shared piece / position
- each turn: player chooses an outgoing edge
- player who can't make a move: loses
- two players w/ starting vertex
- example board
- DAG game: a game w/ loopless DAG
graph LR
1(( ))
2(( ))
3(( ))
4(( ))
5(( ))
6(( ))
7(( ))
8(( ))
9(( ))
10(( ))
11((L))
1-->2
2-->3
1-->4
4-->3
1-->5
5-->3
3-->6
3-->7
7-->8
8-->9
8-->10
9-->11
10-->11
- play: a path on a DAG
- assume: both players are smart / doesn't make mistake
- = optimal play
- properties
- game: always ends
- because: there is no cycle
- and thus, there are at most (tree-like) steps
- because: there is no cycle
- every vertex: either or (win / lose)
- generally: if it has edge to vertex: it is a
- if it only has edge to vertex: it is a
- generally: if it has edge to vertex: it is a
- game: always ends
- successor: vertices that a vertex has (directed)
-
Rooted trees
- rooted tree: tree , in which : chosen as root
- s.t. it is ordered: from root to outwards
- 👨🏫 sometimes it's the other way
- tree: can be thought of a descendants, etc.
- 👨🏫 interestingly, we often locate tree at the top
- vertex without a successor / child: leaf
- 👨🏫 definition of leaf: varies
COMP 2711H: Lecture 16
Date: 2024-10-07 18:00:56
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Extra Problems
-
Problems
- following problems: easy on trees, hard on general graph
- explanation: on 3721
- 👨🏫 for now, trust me :p
-
Problem 1: Longest path
- input: graph
- output: longest path in
- lemma: given a tree, then longest path in
- = -path where are leaves
- if it's not a leaf, it must have an extra vertex that is a leaf
- as a tree can't have a tree
- then, we can extend the path to that leaf
- algorithm:
- pick any non-leaf vertex as root
- turn tree into a rooted tree
- we can: do case work on highest point
- 👨🎓 or: lowest common ancestor
- assign depth to all nodes
- depth: maximum nodes one can go down until it reaches the leaf
- = dynamic programming in 3711
- but it's just another way of computing for now
- : length of longest path which highest vertex is
- longest path w/ as the highest point: either
- max depth[v]
- 2+max depth[v]
- 2+2nd-max depth[v]
- 👨🏫 "try" to solve it on general graph
-
Problem 2: Maximum independent set
- set
- s.t.
- i.e. subgraph without any edge connecting them
- input: graph
- output: largest possible size of independent set
- if input is a tree, algorithm:
- pick any arbitrary as root
- : subtree of rooted at
- 👨🏫 but, doesn't help solving it directly
- : size of the largest independent set
- s.t.
- : size of the largest independent set
- s.t.
- output:
- but, how can we compute each cases?
- for a leaf :
- for a non-leaf:
- strategy: compute for all leaf
- if all of a node's children are computed
- then compute the node
- if all of a node's children are computed
- set
-
Problem 3: (Huffman) Coding
- exists: a file consists of words
- a coding is:
- file:
"abcaaabcaaa"a: being repeated multiple times- let's say, we map:
- but at current stage: it cannot be recovered
- e.g.
0101can beabababccabcc
- e.g.
- we want: prefix-free code
- no : a prefix of a ()
- e.g.
100100: only maps toabc
- or, we can compress it better
- more compact, thanks to 1-bit
a
- what is the most cost-effective code?
- how can we find so?
- 👨🏫 codes can be represented as a tree
- example tree
graph TD
1((ε))
2((0))
3(( ))
4((10))
5((11))
1--0-->2
1--1-->3
3--0-->4
3--1-->5
- as we want to minimize the length
- what should we do? based on frequency
- 👨🏫 Huffman's algorithm!
- Huffman's algorithm
- suppose: word appears times
- sort words based on
- merge the two least frequent words (in a tree)
- create a Huffman tree on words
- then repeat recursively
- example process
- now: assign
0to one, and1to another - finally
graph TD
0(( ))
1((a))
2(( ))
3((c))
4(( ))
5((b))
6(( ))
7((d))
8((e))
0--0-->1
0--1-->2
2--0-->3
2--1-->4
4--0-->5
4--1-->6
6--0-->7
6--1-->8
- proof of correctness: is this optimal?
- let's say, we are given an ideal coding
- the least frequent words: we want it to be far down as possible
- lemma: take: leaves are farthest from the root
- show that such two nodes must be a sibling
- or else: i.e. farthest leaf's parent has only one child
- than we can simply replace the parent with leaf node
- and that is enough: optimal way to code sibling are
0,1- path to least-frequent sibling's parents
- +1 (for child)
- actually:
- induction on no. of words
- base case: 2 words
- ❓ can we parallelize the unpacking process?
- 👨🎓 simply: putting separators every bytes
COMP 2711H: Lecture 17
Date: 2024-10-09 14:52:53
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Distance in Graphs
-
Distance
- distance : minimum number of edges in -path
- or: length of -path
- eccentricity of :
- i.e. maximum distance from
- center of graph: s.t.
- radius: maximum distance from center
- diameter: maximum distance within the graph
- distance : minimum number of edges in -path
-
Theorems on graphs
- theorem: for any graph :
- proof:
- left inequality: trivial
- It cannot be the case that
- center has max distance to (one used for diameter)
- and must be able to connect at distance at least
- theorem: if a tree w/ 3 or more vertices:
- no leaf can be a center
- proof:
- suppose a leaf and its parent
- then for all
- thus cannot have minimum eccentricity
- theorem: let be tree. it has either 1 center or 2 neighboring centers
- proof
- base case:
- 1 vertex: has 1 center
- 2 vertices: has 2 neighboring center
- (strong) induction: for nodes w/ vertices
- we know that leaf cannot be center, thus we eliminate them
- then, for all that's remaining,
- thus center does not change in any case
- as new tree has less vertices, it is true
- or: after repetition, it leads to base case
- base case:
- theorem: for any graph :
Single-Source Shortest Paths
-
Single-source shortest paths
- let input: graph with vertex
- we want output: for all
- solution 1: breath-first search
- BFS: explores all vertices at distance 0 first
- then 1, 2, and until all in CC are discovered
- (max: rounds)
- BFS: explores all vertices at distance 0 first
- solution 2: path length calculation
- let :
- distance: can be expressed as smallest w/
- : all neighbors of
-
Weighted graphs
- for weighted graph w/
- length of path :
- and distance given by:
- initial weight:
- ,
- : path not defined
- for
- for weighted graph w/
-
Adjacency matrix representation
- adjacency matrix :
- if no -edge exists:
- example
- adjacency matrix :
graph LR
1((1))
2((2))
3((3))
4((4))
1--2---2
1--1---3
2--6---4
3--0---4
- : shortest walk with one edge from to
- for steps:
- 👨🏫 a 'modified' matrix multiplication
- multiplication into addition
- sum into
- 👨🏫 a 'modified' matrix multiplication
- for there to be step walk from to :
- must be step walk from to , and edge between to
- for steps:
- new matrix multiplication
- logically, we obtain
-
- as any 100 step path: can be divided into two 50 step paths
-
- finally, can be computed by:
if t = 1: return A if t = 0: return I // only valid path: to itself if t is even: B = pow(A, t/2) return B × B if t is odd: B = pow(A, ⌊t/2⌋) return B × B × A - then distance can be computed by
- w/ shortest walk on edges
- to support shortest walk w/ at most edges
- self-loops can be added to each vertex
- in this case, we have:
-
- any CC: must be connected in edges at least
- : no. of vertices
Dijkstra's Algorithm
-
Dijkstra's Algorithm
- Input: weighted graph and vertex
- w/ non-negative edge weights
- Output: distance for every vertex
- intuition
- check vertex
- for all of its neighbors: update its weight
- for a walk with minimum length (say: ):
- shortest walk for two vertices are finalized
- as all other alternatives: longer than
- then, update weights for all of 's neighbors, repeat
- rough pseudocode
- initialize distances: for all
- create a priority queue containing all vertices in
- while is not empty:
- extract vertex w/ minimum distance from
- for each neighbor of :
- if :
- update the priority of in
- if :
- initialize distances: for all
- Dijkstra's algorithm: results in a spanning tree
- prove that it is indeed shorted path
- Input: weighted graph and vertex
Matchings
-
Matchings
- matching
- s.t. no two edges in sharing an endpoint
- not necessarily covering all vertices
- example
- matching
graph LR
1(( ))
2(( ))
3(( ))
4(( ))
5(( ))
1-->2
2--M-->1
1-->4
2-->3
3--M-->4
4-->3
4-->5
-
Types of matchings
- : maximal matching if
- cannot add any more match
- example
- : maximal matching if
graph LR
1(( ))
2(( ))
3(( ))
4(( ))
1-->2
2--M-->1
2-->3
3--M-->4
4-->3
- : maximum matching is
- all maximum matching: maximal
- not the other way around
- example
- all maximum matching: maximal
graph LR
1(( ))
2(( ))
3(( ))
4(( ))
1-->2
2--M-->3
3-->4
- maximal (cannot add anymore), but not maximum
-
Alternating walks and augmenting paths
- suppose: being a matching in
- alternating -walk: defined at
- walk that alternates between edges in the matching and edges in the set
- 👨🎓 ~=changing group every turn?
- augmenting walk/path: alternating path starting & ending in
- augmenting edge: cant be used for expanding the matching
- simply: swap the colors, within the alternating path
-
Theorem on maximum matchings [Berge]
- theorem: a matching is maximum iff it does not contain an augmented path
- proof:
- if there is augmented -> not maximum: trivial
- as stated above
- not maximum -> augmented
- let be a non-maximum matching
- let be a maximum matching
- let
- s.t.
- i.e.
- and let : a graph
- degree of : at most 2
- i.e. one from , another from
- s.t.
- previously: a graph w/ degree at most 2: made of cycles / paths
- for a cycle (w/ every edge having degree 2)
- it must be an even cycle
- as and within it must alternate all the time
- however, as , there must be a path
- starting with and ending with
- which is an augmented path for
- if the matching was maximum: there won't be an augmented path
- for a cycle (w/ every edge having degree 2)
- if there is augmented -> not maximum: trivial
COMP 2711H: Lecture 18
Date: 2024-10-14 09:02:26
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Matchings (cont.)
-
Matching
- matching: set that no two edges share an endpoint
- suppose: graph is bipartite
- w/ parts
-
Bipartite and Matching
- what is condition for having a matching covering all ?
- consider
- if are bipartite:
-
- as they must be at least one edge from to
- theorem (Hall): in an
- there is a matching saturating iff.
- proof
- matching -> for all: trivial
- forall -> matching
- check: maximum matching
- let : be maximum matching
- suppose: does not cover all of
- then: it implies there is an edge connecting to another
- s.t. is not included in
- and being neighbor of
- take all alternating path from
- : has no matching
- thus it starts with non-matching edge
- then we must have a matching edge from to
- then a non-matching edge from to
- matches with completely
- : has no matching
- but, for there to be a perfect matching:
- as a pair for : must exist
- : can't be neighbor of
- that way we can extend the matching
- : can't be neighbor of either
- such does not exist
- and thus, that is not
- corollary: let be a -regular bipartite graph
- , has a perfect matching
- no. of edge:
- suppose
- what is no. of edges between and ?
- yet, not all edges of goes to
- thus:
- what is condition for having a matching covering all ?
-
Vertex cover
- vertex cover: set of vertices s.t. every has at least one endpoint in
- 👨🏫 easy to find a large vertex cover
- just like how easy is to find a small matching
- let be matching, a vertex cover
- if there is a vertex
- theorem: in every graph ,
- let there be a cycle
- is there a case:
- for an odd cycle:
- theorem (König): in every bipartite graph ,
- proof:
- : shown
- now prove:
- let be a minimum vertex cover
- however, there can be no edge between and
- that way we have a larger matching
- implying that is not a minimum VC
- yet, there can be an edge between
- some edge will be lost when we separate
- some edge will be lost when we separate
- suppose
- how many neighbors does have in ?
-
- if , there is an unnecessary vertex in
- union of matching with : matching over overall
-
Independence
- a set s.t. no edge has both endpoints in
- theorem: is a VS iff is on I.S. (independent set)
- as will be a VS
- theorem: in any graph w/ vertices:
-
- as they are complementary
-
-
Edge cover
- edge cover: subset of s.t. every vertex is incident to at least one edge in
- now all graph has an edge cover
- e.g. when there is an isolated vertex
- 👨🏫 a (stupid) corner case
- e.g. when there is an isolated vertex
- it is easy to find a large (e.g. )
- what is the minimum edge cover?
- discovery so far:
- for any graph
- in bipartite
- without isolated vertices (Gallai)
- 👨🏫 kind of funny: sum on size of two "edge" sets = size of all vertex
- for bipartite w/ no isolated vertices
- 👨🏫 simple math!
- for any graph
- Gallai theorem
- part 1: w/ matching of size , there exists an edge cover of size (at most)
- every edge in matching: covers 2 vertices
- and edges outside : might be connected as well
- part 2: if we have an edge cover of size
- then we have a matching of size (at least)
- edge cover: minimal if there is no stupid = unnecessary edge
- stupid edge: for , only covers its two endpoint
- that are already covered without
- stupid edge: for , only covers its two endpoint
- suppose: a minimal edge cover w/ edges
- let
- then degree of : can be high degree, too
- e.g.
- part 1: w/ matching of size , there exists an edge cover of size (at most)
graph TD
0(( ))
1(( ))
2(( ))
3(( ))
4(( ))
5(( ))
0---1
0---2
0---3
0---4
0---5
- all connected components: **star**
- i.e. tree with central point
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span></span></span></span>: a collection of starts
- how many starts o we have?
- w/ <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span></span></span></span> edges and <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">n</span></span></span></span> vertices
- have <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6667em;vertical-align:-0.0833em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span></span></span></span> connected components
- as <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span></span></span></span> is a forest
- no. of components <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.7778em;vertical-align:-0.0833em;"></span><span class="mord">+</span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">n</span></span></span></span>
- finally, picking an edge from each CC: gives matching of size <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6667em;vertical-align:-0.0833em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span></span></span></span>
COMP 2711H: Lecture 19
Date: 2024-10-14 22:27:53
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Network Flow and Ford-Fulkerson Algorithm
-
Matching (cont.)
- design an algorithm giving a maximum matching
- pick any trivial matching: empty or maximal matching
- if it's not a maximum: search for an augmented path
- while such path exists: expand the matching
- finally, if no augmented path can be found
- it's a maximum matching
- similar technique: starting with suboptimal solution
- and keep improving the method
- 👨🏫 still "augmented"
- until it can't be further improved
- theorem: if it can't be further improved => it's optimal
- and keep improving the method
- design an algorithm giving a maximum matching
-
Network flow
- problem of interest: network flow
- directed graph
- w/ capacity function
- claim: there are two special vertices
- source and sink
- example
graph LR
a((a))
b((b))
c((c))
d((d))
a--4-->b
a--5-->c
b--6-->d
b--1-->c
c--5-->d
- source: <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">a</span></span></span></span>
- sink: <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord mathnormal">d</span></span></span></span>
- 👨🏫 consider: edge as unidirectional water pipe
- and capacity: of water flow
- question: what's the max possible flow from source to sink, s.t. all water reaches sink?
- 👨🏫 name: maximum flow algorithm / max flow
- from above example: has capacity , thus we can't send flow larger than 4
- instead of edge: assign capacity to every pair of vertices
- ~= Dijkstra?
- now:
- flow: function
- : flow from to
- condition / constraints
-
- skew symmetry
- sending 2 units : same as sending -2 units
-
- all except source & sink: indegree = outdegree
- preservation of flow: water coming out from source = water reaching sink
- for source:
- there may be edge to source as well
- and for sink:
- solution , flow s.t. it satisfies 3 conditions above:
- intuition
- for a walk: total flow that can be pass through it = minimum capacity of an edge in walk
- e.g. 1 unit across
- capacity: 4,1,5
- e.g. 1 unit across
- interestingly: one can send flow in reverse direction, too
- e.g. 1 unit across
- capacity: 5,-1,6 respectively
- as it "cancels" my previous flow
- e.g. 1 unit across
- formally speaking:
- if there is flow
- then
- and , satisfying condition
- if there is flow
- thus: find a path
- using only the edges:
- for a walk: total flow that can be pass through it = minimum capacity of an edge in walk
- residual graph of flow :
- w/ same vertices as
- any non-zero edges on this graph: can be utilized for more flow
- upon move :
- and
- is there a case: our flow is maximal, but not maximum?
-
Ford-Fulkerson's algorithm
- basically the idea above
- start with initial flow as 0
- while there exists an augmented path from the source to the sink
- find an augmenting path using any path-finding algorithms
- BFS or DFS
- determine: amount of flow that can be sent along the path
- i.e. minimum residual capacity along the edges of the path
- increase the flow along the augmented path by determined amount
- find an augmenting path using any path-finding algorithms
- return the maximum flow
-
Proof of correctness
- first: extend
- s.t. for a set :
- and
- suppose:
- then,
- define: cut in : division
- s.t.
- what is is : a cut?
-
- as for any non- :
-
- (due to condition)
-
- as sum of flow from any non- vertex: 0
- , almost by definition
-
- similarly, define for vertex group
- then: (as inequality holds for every elements)
- a flow is optimal if (can't be further improved)
- thus: find a cut satisfying the condition
- let : all set of vertices that an be reached from in residual graph
- and the rest:
- as algorithm continued until you can't reach in residual anymore
- when the algorithm is stuck: there is no edge going
- if there was: it's reachable, and thus marked
- as original graph and residual graph: shares vertices, but not edges
- there "might" be an edge
- but its non-existence in residual: shows that all its capacity has been used up
- how about ?
- in original graph, it might have
- however: in can't have positive flow as that would add positive edge in residual graph
- which is edge, impossible
- finally:
- thus: the algorithm outputs optimal solution
- related idea: it also gives minimum capacity with
- does this algorithm runs forever?
- if flows doesn't start with 0 / set is of real numbers: yes
- each step: increases flow at least by one
- new range of
- furthermore, upper bound for flow exists: capacity
- thus it can't run forever
- if flows doesn't start with 0 / set is of real numbers: yes
- 👨🏫 in 3711, you make it run for w/ slight modification
- first: extend
COMP 2711H: Lecture 20
Date: 2024-10-16 22:28:14
Reviewed:
Topic / Chapter: Stable Matchings and Graph Coloring
summary
❓Questions
Notes
Stable Matchings
-
Problem reduction
- given: bipartite graph
- return: maximum matching
- can we: leverage the fact that the graph is bipartite?
- idea: convert bipartite graph to max flow problem
- let all edge between to be directed
- add a source , connect to all vertex
- add a sink , connect to all vertex
- for all edge: direction is left to right
- all with same capacity
- claim: maximum flow in this new graph, : gives size of maximum matching in
- strategy: prove that two are to each other
- assume: original matching exists in
- then: as no two endpoint overlaps, one can create a flow based on it
- without going over the capacity
- for any matching, there is a flow of same size (= sharing common edges)
- thus max matching <= max flow
- then: as no two endpoint overlaps, one can create a flow based on it
- the other way: a flow exists in
- where unit:
- and consider: only flow / edge in bipartite points
- all edge w/ flow = 1: makes a corresponding matching
- as capacity of all edge: 1, no valid flow can have any conjunction (e.g. )
- max matching >= max flow
- 👨🏫 overall idea: reduction
- algorithm solving one problem: can solve another problem
- regardless of details of algorithm
- we: reduced maximum flow into maximum matching
- 👨🏫 you can somewhat claim: max flow is a harder problem
- algorithm solving one problem: can solve another problem
-
Stable matchings
- e.g. man and women
- want: a perfect 1-to-1 matching
- problem: everyone has preferences
- e.g. every woman : has a preference - permutation of man
- same for man
- all: willing to marry
- suppose: is a perfect matching (all men & women: matched)
- and : not matched together
- pair : unstable if
- prefers over current spouse
- prefers over current spouse
- matching: stable if there are no unstable pairs
- theorem: there is always a stable perfect matching
- typical existence proof in graph: elaborate an algorithm finding solution
- and prove correctness of the algorithm
-
Stable matching algorithm
- algorithm: of several iterations
- for every iteration:
- all man propose to a most preferred woman
- (who has not rejected him so far)
- if: every woman has exactly one proposal they all accept; return
- else: every woman w/ more than one proposal reject all except the most preferred one
- yet: doesn't "accept" the top proposer as well
- maybe tomorrow: she won't get any propose otherwise!
- yet: doesn't "accept" the top proposer as well
- all man propose to a most preferred woman
- algorithm: results in a stable perfect match!
-
Proof of correctness
- algorithm: terminates as
- list of woman a man is willing to propose: shrinks
- total sum on size of all list of woman-to-propose: decreases every time
- yet: it can't go down below 0 ( to be precise)
- background
- from man's PoV: preference is going down
- from woman's PoV: preference is going up (better man might get rejected and come down)
- no. of man not getting rejection: increases
- from man's PoV: preference is going down
- proof by contradiction
- suppose is unstable pair
- prefers over current (e.g. )
- and similarly so
- it's impossible as: should have proposed to before
- yet: it was rejected by
- which means: had a better option at the point
- 's current spouse: must be at least better than the previous optimal option
- which means: had a better option at the point
- yet: it was rejected by
- thus: algorithm always produces stable perfect matching
- suppose is unstable pair
- algorithm: terminates as
Graph Coloring
-
Graph coloring
- given graph : a proper coloring w/ colors: a function
- s.t. for every edge : two endpoints of w/ different color
- definition: doesn't matter whether edge is unidirectional or bidirectional
- chromatic number : minimal number of colors
- needed to properly color
- bipartite graph two-colorable
- independent set: s.t. no edge with both endpoints in
- clique: s.t.
- opposite of IS
- complete subgraph?
- smallest IS/ clique: empty / one-vertex set
- question: can we cover any graph?
- 👨🏫 is the graph is simple - if there is no loop!
- having multiple edge between two nodes: doesn't matter
- let: be size of a largest IS
- let: be size of a largest clique
- given graph : a proper coloring w/ colors: a function
-
Theorems
- theorem:
- somewhat obvious, as:
- there must be colors for largest clique alone
- theorem:
- : size of an largest IS
- proper coloring: w/ groups
- thus
- as each group: at most elements
- then:
- finally: let be chromatic number
- theorem:
- e.g. complete graph
- theorem: suppose : graph w/ maximum degree
- algorithm: greedy coloring
- pick a vertex: color it w/ smallest color possible
- (i.e. not used with its neighbors)
- repeat until all are colored
- doesn't return an optimal color
- pick a vertex: color it w/ smallest color possible
- above algorithm: colors w/ at most
- as : at most neighbors
- and thus (even if its neighbors have all distinct colors):
- can be colored with at most color
- and thus (even if its neighbors have all distinct colors):
- as : at most neighbors
- 👨🏫 no particular better upper bound
- e.g. a triangle / odd cycle: max degree being
- and it requires colors
- same for a complete graph: max degree ,
- e.g. a triangle / odd cycle: max degree being
- exists a theorem: only graphs requiring colors are odd cycles / complete graphs
- finding a better order of coloring
- first: sort vertices w/ degree in non-increasing order
- then: color it the same way as primary school method above
- first: sort vertices w/ degree in non-increasing order
- theorem: let a graph w/ degree seq.
- 👨🏫 many theorems in this area: derived from analysis of algorithm (solution)
- assign color 1
- then assign color 1 if is not its neighbor, 2 otherwise
- on : no. of colored neighbors
- as we colored total of items previously: also
- thus: no. of colored neighbors
- then
- finally, largest color used (not necessarily optimal) is
- theorem:
-
Cartesian product
- suppose : graphs
- Cartesian product of two, aka
- rule: if:
- or:
- simple example: grid
- for following
- suppose : graphs
---
title: G, H
---
graph LR
1((1))-->2((2))
2-->3((3))
a((a))-->b((b))
- then <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal">G</span><span class="mord amsrm">□</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span></span></span></span>:
graph LR
1a((1,a))-->2a((2,a))
2a-->3a((3,a))
1b((1,b))-->2b((2,b))
2b-->3b((3,b))
1a-->1b
2a-->2b
3a-->3b
- literally, a grid
-
Theorem
- theorem:
- Cartesian product: cannot have less coloring than operands
- as it's some sort of copy / repeat
- suppose:
- and
-
- example
- and this is a proper coloring in general, as in either case of the rule:
- or:
- we are assigning a new color
- case 1:
- and there is an edge , thus
- as sum are different (and ), is different, too
- case 2: can be done similarly
- instead of
- finally: it's a valid coloring
- Cartesian product: cannot have less coloring than operands
- theorem:
COMP 2711H: Lecture 21
Date: 2024-10-21 09:02:41
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Introduction to Integers ℤ
-
Introduction to
- rules
-
- if
- , then
- 👨🏫 we don't need :p
-
- order: an extension of on N:
- if
- predecessor:
- rules
- addition can be extended similarly
- multiplication
- subtraction
- absolute value
- rules
-
Division
- theorem: let
- there exists unique s.t.
- and
- there exists unique s.t.
- let
- and
- in : well-ordering principle doesn't work
- we want
- s.t. we can argue well ordering principle
- itself is non empty
- , then simply: when
- if : use following lemma
- lemma:
- if : use
- if : use
- if : use
- thus: we can make for arbitrary
- let be minimum element of (exists due to )
- so s.t.
- suppose:
- however, in this case, we can make a even smaller remainder
- by contradiction: this implies
- proof of uniqueness
- proof by contradiction, again
- let following be two different solutions
- if , then
- if and :
- then
- lemma:
- 👨🏫 prove yourself!
- but
- thus contradiction
- then
- theorem: for every , where :
- division by negative number
- there exists unique s.t.
- where
- definition: if
- theorem 2.2:
-
-
- thus
-
-
- use absolute value to prove
- for every
- theorem: let
Greatest Common Divisor
-
Greatest Common Divisor
- 👨🏫 you expected prime numbers? no! GCD first!
- GCD: let , not BOTH are
- unless: all number might be common divisor
- : is iff:
-
- 👨🏫 or equivalently:
- but it will make some of our proof unnecessary
- more interesting :)
- 👨🏫 or equivalently:
- for , finding one is trivial
- find common divisor / intersection of divisors
- and find greatest & positive one
- unlike so: we must also prove existence of
- theorem: for every , not both 0
- s.t.
- proof: let
-
- if : it can be any multiple of another
- otherwise
- thus: has a minimum element,
- : has all properties of
- : divides both
- suppose
- ,
-
- which: is smaller than , thus contradiction
- finally,
- similarly, prove
- thus we have shown
- suppose:
- 👨🏫 furthermore, can be written as linear combination of
- corollary: where not both 0
- relatively prime: iff
- theorem: if then
- the only problem: , but it's given
- theorem: if and and , then
- 👨🏫 only if we had common prime factor, this would have been easier... (but not defined yet)
- thus proven
- ⭐ Euclid's lemma: if and , then
- as ,
COMP 2711H: Lecture 22
Date: 2024-10-21 18:01:38
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Euclidean Algorithm
-
Euclidean algorithm
- theorem: if , ,
- then
- proof
-
- as
-
- as
-
- algorithm
Pseudocode gcd(a,b): if b|a: return b let q,r be s.t. a = q\cdot b + r return gcd(b,r) - C++ way
int gcd(int a, int b) { if (a % b == 0) return b return gcd(b, b % a) } - algorithm: terminates as value of keep decreases
- from 3711H: Euclidean algorithm has runtime
- 👨🏫 quick!
- Euclidean algorithm: explains how to write as linear combination of
- example:
- or, the other way:
- theorem: if , ,
-
LCM: least common multiple
- two definitions possible
- : s.t.
-
- or
- theorem: for
- proof (without prime factorization)
-
- show: satisfies properties of
- using
- where
- thus : common multiple of
- suppose: a common multiple of
- given , then
- and : integers
- thus
- and
-
- corollary: if : then
- trivial: as
Prime Number and Fundamental Theorem of Arithmetic
-
Prime numbers
- an integer : prime if its only divisors are
- notice that: only positive integer excluding is eligible for prime
- theorem: if : prime and then
- if : divisor of => theorem holds
- what if: ? we must show
- , as it would mean
- thus, must be 1, as and
- by Euclid's lemma:
- corollary: if : then
- corollary: if , where are all prime:
- then
- an integer : prime if its only divisors are
-
Fundamental theorem of arithmetic
- for every integer , we can write:
- where every : a prime, and
- not necessarily distinct (e.g. )
- we call this: prime factorization of
- and this is unique for each number
- where every : a prime, and
- proof of existence: strong induction on
- base case:
- consider: prime factorization
- case 1: if prime:
- case 2: if composite:
- let
- , thus prime factorization for exists
- let
- and
- then (sorted)
- proof of uniqueness:
- suppose
- then
- e.g. : can divide all sides
- from corollary,
- eliminate from both sids
- that way, you can continue to eliminate all prime factors.
- 👨🎓 in the end: they must be equal, and you realize that both sides were same from the first place
- for every integer , we can write:
-
More compact notation
- example:
- let
- let
- then:
- then:
- this theorem: makes proof of many previous theorem easy
- e.g.
- theorem: is irrational
- let and , then
-
- as ,
- thus : thus contradiction
- theorem: there are infinitely many primes
- suppose: : all possible primes
- then
- f
- theorem: suppose : -th prime number
- 👨🏫 prove it using induction, and show it holds for all previous primes
- as we know upper-bound of next prime
COMP 2711H: Lecture 23
Date: 2024-10-27 23:59:41
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Congruence
-
Congruence
- congruence: iff
- alternative notation: ,
- example:
- theorem: iff has same remainders when divided by
- proof:
- if , ()
- then
- same, and unique remainder!
- if same remainder
- then
- if , ()
- congruence: iff
-
More theorem
- theorem: let ,
- then following properties hold
-
- proof: ,
- then
-
- proof: ,
- thus
- proof: ,
- (special case of above)
-
- 👨🏫 can be proved using definition
-
- when ?
- 👨🏫 False, counter example:
- yet
-
- applying multiple times
- theorem: let ,
Modular Multiplicative Inverse
-
Modular multiplicative inverse
- if we have multiplicative inverse
- we can cancel, like:
- 👨🏫 which is why division is closed within real numbers:
- all real numbers (except ): has multiplicative inverse
- modular multiplicative inverse : integer s.t.
- MMI: doesn't always exist
- e.g.
- no number s.t. exist
- as: will always be even
- and subtraction of from even no. will return in even no.
- e.g.
- but sometimes exist
- e.g.
- when
- thus:
- as you can multiply 's MMI, on both sides
- e.g.
- if we have multiplicative inverse
-
Finite field
- when calculating , range are
- shift function (all in )
- e.g.
- (modulo)
- claim: shift function is a permutation
- 👨🏫 trivial, but one can prove by showing
- it's one-to-one and onto
- 👨🏫 trivial, but one can prove by showing
- for every permutation: we can create a graph
- e.g. edge from vertex to vertex
graph LR
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
0-->2; 2-->4; 4-->0
1-->3; 3-->5; 5-->1
- graph of permutation: multiple disjoint cycles
- finding an MMI of : must be within the same cycle
- for , it's finding starting from
- also, must be within the same cycle as
- unless: cannot reach how many times we multiply
- to find MMI of , draw cycle again
graph LR
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
0-->5; 5-->4; 4-->3
3-->2; 2-->1; 1-->0
- because <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">5</span></span></span></span> is in the same cycle as <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span>: <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8141em;"></span><span class="mord"><span class="mord">5</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8141em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">−</span><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span> exists in <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">n</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">6</span></span></span></span>
- when are in the same cycle (of )
- multiple of can definitely reach
- as it means
- but, when are and in the same cycle?
- = when there is only one cycle (as can be added to generate other numbers)
- multiple of can definitely reach
- claim: all cycles have the same size
- as every cycle: shift of another
- suppose:
- each cycle: has size
- proof
- let
- then the cycle including :
- all numbers appearing in cycle (including ):
- linear combination of
- which: are always divisible by
- claim:
- then no. of cycles:
- size of each cycle:
- proof
- as
- also appears in cycle involving
-
- 👨🏫 after traverse from , we will find which is effectively
- after traversing times, we reach
- for
- thus the cycle containing contains all multiples of
- so size:
- and as all cycles of same size:
- as
- theorem: has MMI iff
- this case: will be in the cycle
- and thus: all numbers will be in the cycle
- (easier) proof: finding inverse = finding s.t.
- if , can we obtain weaker result?
- theorem: let and
- then
- proof:
-
- apply: Euclid's lemma
- as and
- thus proved
- 👨🏫 graph is more intuitive, yet this is more concise
-
Fast modular exponentiation
- finding :
- e.g.
- stupid way: computing , then computing
- workload would be immense if:
- smarter way
- or:
- pseudocode
pow(a, b, c): if a == 0: return 0 if b == 0: return 1 if b == 1: return 1 % c d = pow(a, b / 2, c) d *= d d %= c if (b % 2 == 1): a %= c # if we want small a d *= a d %= c return d - example: divisibility by
- a number: divisible by iff its digits are divisible by
- e.g. in base 10: number equals
- where : -th digit (from the back, starting from )
- and claim:
- holds as
- 👨🏫: same for 9
- for modulo , it also works it's base (basically any )
- holds as
- what if: we want to compute on base 10 integer?
- as
- thus
- as
- theorem: let : polynomial w/ integer coefficients
- if
- as each
- finding :
Chinese Remainder Theorem
-
Chinese remainder theorem
- linear equation
- solvable iff
- consider: cycle starting w/ for
- : must be in the cycle
- how may solutions to exist if ?
- no. of solutions:
- proof:
- consider: cycle, which has size (as )
- if : must be somewhere in cycle, as
- s.t.
- we can traverse extra times to reach the same point
- 👨🏫 no other solutions!
- as ,
- generally:
- as we want
- for following systems of equation
- assume:
- and
- and
- 👨🏫 to ensure that there will be exactly 1 solution
- find value of satisfying all conditions
- finding solution: is it always possible?
- assume:
- let ,
- then
- and
- can above two equations be combined?
- let solution to individual equations
- then following also holds
- then following also holds
- example
- : 1 solution
- then: create cycle ()
- linear equation
graph LR
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
6((6))
3-->1
1-->6
6-->4
4-->2
2-->0
0-->5
5-->3
- find <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span> (<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8444em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>) from the cycle
- as <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8444em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">⊥</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>, it can always be done
- as <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mop"><span style="margin-right:0.01389em;">g</span>cd</span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mclose">)</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span> is in cycle with <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">0</span></span></span></span>
- and such solution: unique in <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mclose">)</span></span></span></span>
- unique as, within the cycle <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.7333em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal">x</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.8444em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mspace allowbreak"></span><span class="mspace" style="margin-right:0.6667em;"></span></span><span class="base"><span class="strut" style="height:0.8444em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord"><span class="mord mathrm">mod</span></span></span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord"><span class="mord mathnormal">n</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>, there is only place to access <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8444em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal">b</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>
- without repeating
- Chinese Remainder Theorem: can the value be found exactly?
- let : positive integers
- s.t.
- and system of linear congruences exist:
- has: unique solution
- let : positive integers
- above: equivalent to previous statement, as
- , thus exists for
- and we can multiply to both sides
- and let
- , thus exists for
- for , solution:
- proof of uniqueness
- we can merge the first 2 equations
- keep doing so until there are 2 equations (= base case)
COMP 2711H: Lecture 24
Date: 2024-10-28 09:07:24
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Fermat's Little Theorem
-
Fermat's Little Theorem
- theorem: for every prime ,
- one to one: as we can cancel by multiplying both side
- onto: create a program to check
- code
vector<int> seen; cin >> p >> a; // e.g. p = 11, a = 2 int p, a; for (int i = 0; i < p; ++i) if (!seen[i]) { } for (int j = 0; ) - if succeed (primitive root), we will result in: (multiplicative) cycle
- cycle involving only
- cycle involving others
- not always the case: e.g.
- results in cycle size of:
- cycle starting w/ 1: size
- as , : first element star
- code
- cycles will have the same size, except
- as each element: can be seen as
- and thus: elements are divided evenly
- s.t. it's divisor of
- different proof:
- let there be additive cycle of
- which is an equivalent set of
- and multiplying both sides, we get:
- cancelling from both dies, we get
- thus
- let there be additive cycle of
- proof by induction on
- rewrite FLT s.t.
- theorem: for every prime , integer ,
- 👨🏫 now works for too
- claim:
- then: all terms except are congruent to
- lemma:
- claim: it's multiple of when
- as it involves in denominator
- claim: it's multiple of when
- rewrite FLT s.t.
- theorem: for every prime ,
-
Computing modular exponentiation
- for , compute
- (depends on the size of cycle)
- theorem: if then
- simply: take modulus of on exponent
- then check it using the fast modulus algorithm
- for , compute
-
Non-prime number FLT
- assumption breaks: all cycle no longer necessarily w/ same size
- let , define as
- : Euler's totient function
- 👨🏫 not a meaningful name, "how many" or something in latin
- for prime :
- for
- claim:
- intuition: of all numbers: not having in prime factorization
- by multiplying all: we find proportion without common factors
- proof 1: suppose
- for CRT: we obtain "unique solution" for linear system of congruent equation
- 👨🏫 no matter how you choose
- for
- and such numbers within
-
- and manipulate it s.t.
- now, for
- let
- then we have: rel. prime number within
- for
- thus multiply it by , we obtain
- for CRT: we obtain "unique solution" for linear system of congruent equation
- proof 2:
- lemma: if , then
- same as: obtaining solution of system of equation
-
- choose s.t.
-
- choose s.t.
-
- s.t.
- according to CRF, within , we have unique solution for above system
- finally:
- same as: obtaining solution of system of equation
- consider
-
- as numbers are rel. prime to
-
- general case:
- then, for each
- thus:
- lemma: if , then
-
Euler's theorem
- extension of FLT
- let , then
-
-
- one-to-one as can be cancelled from both sides
- : provides cycles (excluding )
- sum of sizes on each cycle
- total size:
- 👨🏫 try to extend other proof of FLT for Euler's theorem
-
Wilson's theorem
- Wilson "guessed" it, not proved it
- but British always have to take fame :p
- for every prime ,
- e.g.
-
- as:
- as:
- second attempt:
- use similar idea:
- as
- 👨🏫 and is the only case
- thus : must include number and its (distinct) MMI as pairs
- naturally:
- lemma: the only s.t. are
- (Euclid's lemma)
- Wilson "guessed" it, not proved it
COMP 2711H: Lecture 25
Date: 2024-10-28 18:04:17
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Symmetric Encryption
-
Symmetric encryption
- Alice: want to send message to Bob
- Eve: can check what's being sent on channel
- encryption scheme
- s.t.
- public: encrypted text, length of original / encrypted text
- old ways: maintaining algorithms private
- problem: leakage requires complete redesign of algorithm
- thus: let based on shared key of Alice and Bob
- algorithm: called symmetric as same key is used for both encryption & decryption
-
One-time pad
- : binary seq. of length
- same for
- let
- then
-
- given , all have the same chance of appearing!
- let
- then
-
- has the same property
- reusing : should be avoided (provides statistical data)
- use RNG from previous value for
- but, how can we have shared key in the first place?
- Diffie-Hellman-Merkle key exchange!
- : binary seq. of length
-
Diffie-Hellman-Merkle key exchange
- procedure: (can be done by either Alice / Bob)
- choose a large prime number (~= 1000 digits), and publish
- from now on: all computation are
- choose a primitive root , and announce
- : p.r. if
- e.g. : primitive root for
- choose a large prime number (~= 1000 digits), and publish
- procedure: (can be done by either Alice / Bob)
graph LR
1((1));2((2));3((3))
4((4));5((5));6((6))
7((7));8((8));9((9))
10((10))
2-->4;
4-->8;8-->5;5-->10;
10-->9;9-->7;7-->3;
3-->6;6-->1;1-->2
- finding primitive root: fairly easy
- choose random number, and check if it is a primitive root
3. Alice and Bob: chooses secret <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">a</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal">b</span></span></span></span> respectively
4. Alice: publishes <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.9444em;vertical-align:-0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.6644em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">a</span></span></span></span></span></span></span></span><span class="mord">%</span><span class="mord mathnormal">p</span></span></span></span>, Bob publishes <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1.0435em;vertical-align:-0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8491em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">b</span></span></span></span></span></span></span></span><span class="mord">%</span><span class="mord mathnormal">p</span></span></span></span>
- system: based on discrete logarithm problem
- which no one knows efficient algorithm
- 👨🏫 yet mathematicians didn't prove it so far
- problem: given <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8588em;vertical-align:-0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.6644em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">a</span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span></span></span></span>, compute <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">a</span></span></span></span>
5. Alice: computes <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1.0435em;vertical-align:-0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8491em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ab</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.0991em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8491em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">b</span></span></span></span></span></span></span></span><span class="mclose"><span class="mclose">)</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.6644em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">a</span></span></span></span></span></span></span></span><span class="mord">%</span><span class="mord mathnormal">p</span></span></span></span>
- and Bob <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1.0991em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.6644em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">a</span></span></span></span></span></span></span></span><span class="mclose"><span class="mclose">)</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8491em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">b</span></span></span></span></span></span></span></span><span class="mord">%</span><span class="mord mathnormal">p</span></span></span></span>
- Eve: cannot compute <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1.0435em;vertical-align:-0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8491em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ab</span></span></span></span></span></span></span></span></span></span></span></span> efficiently
- Diffie-Hellman-Merkle "assumption"
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.0435em;vertical-align:-0.1944em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.8491em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight">ab</span></span></span></span></span></span></span></span></span></span></span></span>
Public Key Cryptography
-
Public key cryptography
- aka asymmetric encryption
- different keys are used for encryption & decryption
- Bob: with key
- : public key, for encryption
- : private key, for decryption
- s.t.
- new protocol: ElGamal encryption
- Bob: chooses a prime , and primitive root , secret value
- and computes
- publishes:
- anyone: can lookup and evaluate
- 👨🏫 non-interactive!
- Alice: to send to Bob
- choose secret , compute
- compute
- sends the result:
- 👨🏫 notice, many people can send message to Bob
- without additional interaction (except decryption)
- Bob: decrypts message by:
- compute
- and subtract it from
- Bob: chooses a prime , and primitive root , secret value
-
RSA
- 👨🏫: why not make keys simpler?
- let
- s.t.
-
- and
- idea: choose random s.t. MMI exist
- Bob: choose
- publish
- Alice: send
- and
- problem:
- thus computing is easy!
- 👨🏫 anyone can decrypt! useless encryption scheme!
COMP 2711H: Lecture 26
Date: 2024-10-30 08:48:22
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Roadmap to RSA
-
RSA: attempt
- currently: we have public encryption key
- and private decryption key
-
- pick random until MMI in field is found
- problem: all knowing can compute
- can we make it harder?
- and rely on the fact: factorization of large number is hard
- currently: we have public encryption key
-
Factorization problem
- inputs: number w/ digits
- (i.e. composite)
- output: "a" factorization s.t.
- algorithm 1
for (a = 2; a < N; ++a) if (N % a == 0) return (a, N / a)- simple analysis: trying at most values
- actual runtime: if and
- algorithm 2: checking primality
for (a = 2; a < √N; ++a) if (N % a == 0) return false return true- run time: won't terminate in decades, even if
- integer factorization: tried for 100s of years
- no one "knows" the efficient solution
- nor was proven
- RSA: depends on this fact
- inputs: number w/ digits
RSA
-
RSA algorithm
- named after Ron Rivest, Adi Shamir, and Leonard Adleman
- key generation
- pick two large primes: (secret)
- all calculations:
- pick , let
- computation of : requires factorization of
- prevents the previous attack
- no proof: RSA assumption
- only given , computing is hard
- computation of : requires factorization of
- announce
- encryption / decryption
- ()
-
- 👨🏫 if message is sent: one can take of the message and \
- then factorize it
-
- where
- 👨🏫 if message is sent: one can take of the message and \
- 👨🏫 is necessary?
- with CRT, to have
- it is sufficient to have:
-
- then
- (instead of )
- again, RSA assumption:
- given and of many
- one cannot decrypt any message unless are known
- 👨🏫 knowing or : leads to finding another and
- 👨🏫 knowing , you can directly decrypt it!
- vulnerabilities exist for "special cases" (not general case)
- e.g. for format , etc.
-
Proof of security
- Bob: holds
- publishes
- Alice: compute
- Eve: cannot compute
- 👨🏫 meet our friend: Dave
- Dave: can manipulate the message over channel
- Alice: sends , encrypted for Bob
- then:
- thus Dave: can replace message with
- potential vulnerability
- with traditional email protocol: such vulnerabilities can be manipulated
- (without digital signature)
- e.g. fake email services
- 👨🏫 you can claim to be other people / email address
- just don't use my email for it :p
- Bob: holds
Digital Signature
-
Digital signature
- let be a message
-
- invalid / valid
- property: only Alice can sign
- yet, everyone can verify signature given
- let verification encryption (as all can do)
- and let sign decryption (as only Alice can do)
-
RSA signature
- simply using RSA encryption / decryption for digital signature
- a "safer" signature, thus:
- whenever sending message, attach digital signature on the way, too
- similar vulnerability exists
- 👨🏫 you must ensure that message: following a particular format
- e.g. starting with 10
0s- or starting with:
I am Alice and my message is: {msg} - multiplication of two messages: results in invalid (protocol wise) message
- or starting with:
- e.g. starting with 10
- furthermore, you must use different key for encryption & signature
- as signing = decrypting
- publishing signature of a message = publishing decryption of a message
-
Example situation
- now Alice, having:
- secret:
- i.e. Alice's secrete key for encryption / signature
- public:
- secret:
- to send from Alice to Bob:
- compute
- 👨🏫 actually: using instead
- let (concatenation)
- let
- compute
- now Alice, having:
- for bob to receive
- 👨🏫 can do it the other way: encrypt-and-then-sign or so
- but ensure that you are using a correct key and modulus
- as separate modulus exist for a pair of keys!
- common error found in the blockchain course
- wrong modulus results in a garbage value
COMP 2711H: Lecture 27
Date: 2024-11-04 08:57:34
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Sets
-
Sets
- naive comprehension (possibly leading to paradoxes)
- writing set with
property/formulaandelement (thing) - 👨🏫 above notation: only works if condition can be written as
- writing set with
- Russell's paradox
- let
- , not
- then let
- must be a "set", as it's defined by comprehension
- paradox: ?
- if : it means (not in set satisfying )
- if : it means (in set satisfying )
- only way out: show that such doesn't exist
- let
- naive comprehension (possibly leading to paradoxes)
-
ZFC
- i.e. Zermelo-Fraenkel (Axioms) choice
- creating a new set from an existing set
- not necessarily all setts hat can be created
- language must be defined, supporting:
- arbitrary no. of variables over sets
- everything: sets
- logical & boolean operators
- only is needed
- others, e.g. , can be derived
- only is needed
- parenthesis
- arbitrary no. of variables over sets
-
ZFC axioms
extensionality: two sets are equal iff they have the same elementsempty set: there exists a set with no elements-
- 👨🏫 : a syntactic sugar
-
unordered pair: if are sets, there is a set- w/ elements are exactly
union: if a set, set consisting of all elements of all the elements of- e.g. for
- 👨🏫 uniqueness of
ZF3,ZF4can be shown - notation:
comprehension: from a universal set- if a formula in
- w/ free variables
- and a set and are sets
- then following is also a set:
- subset of satisfies condition
- 👨🏫 limited version of original comprehension
- original problem / paradox doesn't exist as
- there is no "super set" or set-of-all-sets
- 👨🏫 not everything that can be written in is a set
- 👨🏫 now, it's Russel's proof instead of paradox
- if a formula in
powerset: let be a set. there exists a set whose elements are subsets of- denote
-
Supplementary
- theorem: there is a unique set w/ no elements (w/
ZF1,ZF2)- by
ZF2, there exists a set w/ no elements - let be a set w/ no elements
- for any , and
- thus, following holds (no premise holds)
- by
ZF1, - empty set: will be notated as
- e.g.
- technically not in our language as is included
- yet, we can use as a variable and write equivalent:
- e.g.
- by
- ZF3: set creation
- from , can be obtained
- from , can be obtained
- and so on...
- ordered pairs: w/ : define
- theorem: let be sets,
- 👨🏫 not so trivial proof
- proof
- case 1:
- then (claimed by left side of iff)
-
- thus ,
-
- thus ,
- case 2:
- 👨🏫 trust me, it's case 1
- case 3:
- thus: i.e.
- i.e.
- for
- and for
- thus: i.e.
- i.e.
- case 1:
- extending union
- class
- class: collection of form
- 👨🏫 needed as all operations are only defined on sets
- subset
- Cartesian product
- let be sets
-
- 👨🏫 paradox-prone comprehension!
- use
- RHS: valid formula in now
- , ,
- 👨🏫 Russel said: accepting one paradox implies all other paradox
- e.g.
1=2, then I'm the Pope - building system without paradox: important
- e.g.
- relation
- relation from to : subset
- function
- relation : a function
- if
- relation : a function
- theorem: there is a unique set w/ no elements (w/
COMP 2711H: Lecture 28
Date: 2024-11-04 18:02:47
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Number as Sets
-
Number as sets
- (natural) numbers: can be notated as set
- example
- ...
- def: if as set
- def: a set : inductive if
- d
- (natural) numbers: can be notated as set
-
ZFC axioms
infinity: there is an inductive setreplacement: if is a class function and a set- there is a set containing exactly s.t.
foundation: every set contains an -minimal element- 👨🏫 kind of a base case, a set that cannot be opened any more
- alternatively:
- creation of Frankel
- d
-
Supplementary
- there is a unique set s.t.
- is inductive
- is contained in every inductive set
- proof: let to be an inductive set (from axiom on infinity)
- w/ comprehension:
- this part: trivial
- show: is inductive
- , and
- , and
-
- as one is subset of each other: two are equal
- w/ comprehension:
- let be a formula in s.t.
- then is called a class function
- theorem: let be a set, then
- suppose
- let
- // i.e. non-empty set
- also: cannot be an empty set
- as it must be a number
- there is a unique set s.t.
-
Cardinality of the sets
- finite set: set is finite if there is a function
- s.t. is one-to-one, onto
- infinite set: set without one-to-one correspondence, if is not finite
- let be two sets
- we can write: iif there is a 1-1 and onto functions
- conditions
-
- e.g.
- theorem: let be set of even numbers;
- theorem: let : set of primes,
- as
- theorem:
- assign orders in
- traverse them by:
- and we can assign natural number to them
- assign orders in
- define: if there exists one-to-one function
- prove:
- theorem:
- set: countable if:
- a set has same size to natural numbers
- theorem: let be a countable set
- and also countable
- then: is also countable
- prove: countable no. of countable elements: countable
- : countable
- finite set: set is finite if there is a function
COMP 2711H: Lecture 29
Date: 2024-11-06 09:01:05
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Size of Sets
-
Size of sets
- is there is bijection
- is there is injection
- set : finite if
- infinite if it's not finite
- suppose: and
-
- 👨🏫 an image of
- result in applying on all elements of
- set : countable if
- 👨🏫 at least for this course!
-
Theorem
- theorem: countable sets are the smallest infinite set
- i.e. if finite:
- lemma: if is infinite and , then is also infinite
- suppose: is finite
- which means:
-
- s.t. it's 1-1 and onto
-
- s.t. it's also 1-1 and onto
- thus: is finite (contradiction)
- pick a smallest element
- by lemma above: is infinite
- pick , is infinite
- ... can be continued
- above step: result in an infinite sequence
- as it's a sequence: it's countable
- then
- theorem: if is countable and , then is countable
- let new mapping:
- 👨🏫 similarly, by adding , or finite, items to countable , the result is still countable
- proof: use one by one
- theorem: if countable: so is
- assume
- or else: let
- then
- i.e. even numbers
- similarly,
- i.e. odd numbers
- 👨🏫 then combine!
- suppose: and are bijection
- let be defined as
- 👨🏫 's disjoint condition is used here: cannot assign two values!
- assume
- theorem: let be a countable set
- whose every element is also a countable set
- then is also countable
- proof
- : a bijection
- : a bijection
- consider
-
- two indices, and each map: size
- 👨🏫 finally: is a bijection
- again, must be disjoint for it to be one-to-one
- yet: every case can be reduced to disjoin case
- and
- where is bijection
- 👨🎓 use similar idea as in being countable
- is also countable
- and :
- i.e.
- ,
- 👨🏫 we haven't proved that though
- can't we just say is countable
- and ?
- and :
- theorem: let
- every natural number: w/ unique factorization
-
- and
- define s.t. it's one-to-one and onto
- first try:
- problem:
- or
- thus: not really one-to-one
- problem:
- second try: if and ending w/
0s- define as w/ its last elements removed (no extra 0)
-
- now: it's , which is countable
- 👨🏫 corner case on all-0 and one-0 exists
- theorem: let
- : infinite, and not countable
- 👨🏫 some infinities: are larger than other infinities
- 👨🎓
animal farm
- 👨🎓
- let : be bijection
- each function: can be written as binary mapping
- one can make:
- or reversing at -th index
- 👨🏫 diagonalization
- , thus
- thus: is not onto: contradiction
- conclusion: is not bijection
- theorem of Cantor
- for every set :
- 👨🏫 even for :
- proof: suppose is a bijection
- consider:
- then: either , or
- case 1:
- case 2:
- thus: is not onto: not covering
- 👨🏫 doing the same thing, without relying on countability
- 👨🏫 as we can apply it multiple times
- there are infinite sizes of infinite
- for every set :
- theorem of Tarski
- let : be a set and
- s.t.
- there exists s.t.
- proof
- set : expansive if
- let be a set of expansive sets
- then every expansive
- thus : expansive
- let , thus
-
- union of all expansive sets
- show:
- is expansive, thus
- claim: is expansive
- however:
- and thus
- theorem (Schroder-Bernstein): if and
- then
- proof:
- cut into
- : domain of
- similarly: cut into
- : domain of
- goal: find and s.t.
- then let
- 👨🏫 show that this function is increasing, and use Tarski's fixed point theorem
- cut into
- theorem: countable sets are the smallest infinite set
COMP 2711H: Lecture 30
Date: 2024-11-11 02:56:43
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Rational Numbers
-
Rational numbers
- for
- a rational number: all numbers that can be written as a fraction
- can be expressed as ("expansion")
- decimal expansion of rationals
- similarly: an infinitely repeating one: e.g.
- aka repeating decimal expansion
- 👨🏫 terminating / repeating decimal expansion: can be converted to a rational number
- and vice versa
- theorem: suppose : a terminating / repeating decimal expansion
- then
- case 1:
- case 2:
- 👨🏫 combination of two: also trivial
- theorem: let and
- then has a decimal representation: either terminating or repeating
- case 1:
- 👨🏫 10: our base
- w/ Euler's theorem:
- let
- 👨🏫 also: easy to show that only digits are needed
- : of digits
- case 2:
-
Order
- yet: cannot express all number
- e.g.
- 👨🏫 real numbers will be discussed later
- order: property of set: relation , s.t.
- , we have exactly one of
- , , or
- d
- , we have exactly one of
- precise definition on minimum element
- let : an ordered set,
- element: : an upper bound of if:
- let : set of all upper-bounds of
- and let minimum element of : an supremum of ()
- if there exists s.t.
- then: an supremum of :
- let
- , then
- i..e maximum
- any infinite set:
- , then
- let
- , then
- ordered set : has supremum / least-upper-bound property if:
- every non-empty subset of : w/ an upper bound: also has a supremum within it
- does : have the least-upper-bound property?
- 👨🏫 yes
- assume: be bounded above
- upper bounds of
- by assumption (of bound):
- and every non-empty subset: has minimum element
- which is reachable
- thus: must also have the least upper bound property
- does have one?
- let : an upper-bound for ()
- 👨🏫 assume , and it will lead to infinite descent, etc.
- : doesn't have least upper-bound for
- theorem: , then : a lower bound for if
- ,
- and s.t.
- then: : infimum of
- 👨🏫 i.e. largest lower bound property
- theorem: if an ordered set w/ least upper bound property
- then : also satisfies largest lower bound property
- proof: let and : bounded below
- let : set of all lower bounds of
- 👨🏫 must not be empty: as it is "bounded below" and lower bound exists
- (supremum)
- let
- every : an upper bound of
- :
- 👨🏫 by definition:
- let : set of all lower bounds of
- ⭐👨🏫 thus: having infimum property implies supremum, and vice versa
- yet: cannot express all number
-
Real number
- let set
COMP 2711H: Lecture 31
Date: 2024-11-11 17:53:22
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Real Numbers
-
Real numbers
- every : w/ an infinite decimal expansion
- i.e. non-zero entries forever:
- interval definition: for
- and so on for
- only can be used for
- theorem: if and
- then
- and
- lemma: is infinite
- consider: and , let be countable
-
- from below theorems (up to "hole"), one can always add new elements in
- consider: and , let be countable
- and
-
- theorem:
- i.e. rationals: are dense in reals
- both : cuts;
-
- there must be a hole!
- theorem:
- theorem: (and all other segments)
-
- then: map
- thus:
-
- size of
- first,
-
- 👨🏫 as all elements to : cut
- the other way: show
- check: whether is in
- if so: otherwise
- put in front of number we can thus construct a one-to-one function from
- : one to one
- check: whether is in
- by Schroder-Bernstein:
- first,
-
Axiom of Choice: ZFC 10
- axioms (equivalent)
- for every two sets , either
- or
- for any relation , exists function
- s.t.
- 👨🏫 but... how can you choose the mapping?
- believe: there is a way to make choice
- for every set , there is a function
- s.t.
- for every set of non-empty disjoint sets
- set s.t.
- : set of a point from each region
- set s.t.
- Zorn's lemma: let be a set s.t. for every chain
- we have
- then: has a maximal element
- for every two sets , either
- a set : is chain if
- maximal element of : an element s.t.
- assuming ZFC 10-5: for any two sets :
- either or
- : all 1-to-1 function s.t. and
- i.e. degree of vertex in : min 0, can be
- there is a maximal function
- claim: it either covers entire , or entire
- finally: if Zorn's lemma holds, ZFC 10-1 also holds (all ZFC 10: equivalent)
- axioms (equivalent)
COMP 2711H: Lecture 32
Date: 2024-11-13 04:45:44
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Probability Theory
-
Probability theory
- experiments (coin flip): will result in
- heads
- tails
- and, as we keep tossing coin's what's the chance of getting a head?
- 👨🏫 can we use the limit for probability? probably not
- limit: might not even exist!
- experiments (coin flip): will result in
-
Monty Hall problem
- one of the doors: have a prize
- selection: in uniformly random
- you choose one door. then, the host opens an empty door that you didn't choose
- then, is it better to change your choice?
- w/ computer simulation: you win w/ without changing
- and with changing
- one of the doors: have a prize
-
Sleeping Beauty
- on Monday: Amir tosses a fair coin
- makes us fall a sleep, w/ medicine that also erases your memory
- if head: wakes us up on Tuesday
- if tail: wakes us up on Tuesday
- then give medicine again, waking us up on Wednesday
- if you compute the probability based on no. of "wake up"-s
- the chance: seems like , for head and tail
- due to our non-rigorous definition of probability
- 👨🏫 philosophy people still talk about this
- the chance: seems like , for head and tail
- on Monday: Amir tosses a fair coin
-
Cancer test
- a novel cancer test: accuracy is as of following
- if you have cancer: you get
+w/ 90 percent - if you don't have cancer: you get
-w/ 90 percent
- if you have cancer: you get
- you: take test and gets
+, what's the chance that you actually have a cancer?- 👨🏫 solution: depend on portion of population w/ cancer
- a novel cancer test: accuracy is as of following
Measure
-
Measure
- what is: measure of every subset?
- and we can: assign measure - a weight - on each subset
- first: we have extended :
- then positive extended :
- let : a set (universe) and
- measure : a function
- : a measure space if:
- , and
- let be a countable set of pairwise disjoint sets
- each: , thus measurable
- 👨🏫 with this only, you can't compute from
- if , then
- from second axiom:
- Lebesgue measure
- for every segment from : the measure is
-
- i.e. length of the whole real number:
- what is: measure of every subset?
-
Set & sample space
- let : set sample space
- 👨🏫: convention: uses actually
- sample space: all possibilities
- events
- usually:
- define function
- : a probability space if:
- if being disjoint:
- from 4, 5: u=you can derive
- let : set sample space
-
Conditional probability
- suppose: we know
- then: the information might change the probability
- at least: we cant' say it persists
- as regardless
- definition: let
- define:
- we are defining: a new prob. function
- better notation:
COMP 2711H: Lecture 33
Date: 2024-11-18 08:50:46
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Probability
-
Probability
- probability space: defined by
- : sample space
- : set of events
- : probability (function)
- for any event , conditional probability is:
- : independent events if:
- aka:
- probability space: defined by
-
Example: independent events
- rule: win the game if at least one
Happears - let be 3 events, they are independent if (definition)
- rule: win the game if at least one
-
Example
- For an accident-prone person:
- for normal:
- 👨🏫 and there are two type of people only
- if
- then what is ?
- definition
- let : accident
- : accident-prone
- : not accident-prone (normal)
- 👨🏫 Bayes rule, makes life easier
- compute:
- Monty hall problem
- and
-
- i.e. prize in given prize is not in
- if the strategy: not changing the choice
- then: chance of winning: independent of host's action
- if: door 1 chosen, and door 2 opened by the host
- then: what's the chance that door 1 has the prize?
- For an accident-prone person:
graph TD
0(( ))
1((1)); 2((2)); 3((3))
1_1((2)); 1_2((3)); 2_1((3)); 3_1((2))
0--(1/3)-->1
0--(1/3)-->2
0--(1/3)-->3
1-->1_1
1-->1_2
2-->2_1
3-->3_1
- first row: where the prize is
- second row: the door host will open
- working w/ sample space, we get:
<span class="katex-display"><span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">{(</span><span class="mord mathnormal">x</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span><span class="mclose">)</span><span class="mord">∣1</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8304em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">x</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord">3</span><span class="mclose">}</span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">x</span></span></span></span>: prize
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.625em;vertical-align:-0.1944em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span></span></span></span>: initial choice
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span></span></span></span>: the opened door
- 👨🏫 <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord">∣</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">∣</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">27</span></span></span></span>, yet <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span></span></span></span>: not independent of <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.625em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">x</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel"><span class="mrel"><span class="mord vbox"><span class="thinbox"><span class="rlap"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="inner"><span class="mord"><span class="mrel"></span></span></span><span class="fix"></span></span></span></span></span><span class="mrel">=</span></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.625em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">x</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span></span></span></span>
- not all the cases: w/ the same probability
- case work: <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mclose">)</span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">18</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">18</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">⋅</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">9</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- no choice for <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span></span></span></span>!
- same for <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mclose">))</span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">9</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">18</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">9</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">1</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">((</span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">3</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">2</span><span class="mclose">))</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">18</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">(</span><span class="mord mathnormal">A</span><span class="mord">∣</span><span class="mord mathnormal" style="margin-right:0.05017em;">B</span><span class="mclose">)</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.53em;vertical-align:-0.52em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:1.01em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right:0.13889em;">P</span><span class="mopen mtight">(</span><span class="mord mathnormal mtight" style="margin-right:0.05017em;">B</span><span class="mclose mtight">)</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.485em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right:0.13889em;">P</span><span class="mopen mtight">(</span><span class="mord mathnormal mtight">A</span><span class="mbin mtight">∩</span><span class="mord mathnormal mtight" style="margin-right:0.05017em;">B</span><span class="mclose mtight">)</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.52em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.53em;vertical-align:-0.52em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:1.01em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathnormal mtight" style="margin-right:0.13889em;">P</span><span class="mopen mtight">((</span><span class="mord mtight">1∣2</span><span class="mclose mtight">)</span><span class="mbin mtight">∪</span><span class="mopen mtight">(</span><span class="mord mtight">3∣2</span><span class="mclose mtight">))</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.485em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1/18</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.52em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.53em;vertical-align:-0.52em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:1.01em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1/18</span><span class="mbin mtight">+</span><span class="mord mtight">1/9</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.485em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1/18</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.52em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.1901em;vertical-align:-0.345em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.8451em;"><span style="top:-2.655em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">3</span></span></span></span><span style="top:-3.23em;"><span class="pstrut" style="height:3em;"></span><span class="frac-line" style="border-bottom-width:0.04em;"></span></span><span style="top:-3.394em;"><span class="pstrut" style="height:3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.345em;"><span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal">A</span></span></span></span>: prize in <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.05017em;">B</span></span></span></span>: door <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">2</span></span></span></span> opened
- test: 90% accurate
- then
- let
- i.e. answer depends on how many of population has cancer
- fraction: people got positive & cancer over people got positive
Random Variables
-
Random variable
- real r.v.: function
- s.t. for every segment
- : an event
- : exists
- : a discrete r.v. if : finite / countable
- e.g. dice
-
- let
- then
- translates into
-
Expected value
- for discrete w/
- expectation is defined as
- linearity of expectation: for r.v. (not necessarily independent)
- for discrete w/
-
Example
- w/ being permutation of , inversion s.t.
- suppose: chosen u.a.r.
- no. of inversions in
- what is
- simple solution: all cases are equally likely
- thus: simply sum up all inversion number, and divide by
- use: linearity of expectation
-
- either yes or no
- sleeping beauty (our beloved professor)
- can we "predict" whether it was head / tail?
- strategy 1: always say
- expected reward:
- strategy 2: always say
- expected reward:
- as: w/ , we wake up twice!
- w/ being permutation of , inversion s.t.
COMP 2711H: Lecture 34
Date: 2024-11-18 17:57:54
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Problems
-
Problem 1: expectation of the sum
- toss two fair dice. what is the expected value of the sum?
- each pair: w/ same probability
- you can manually compute, but...
- : no. on the 0th die
- (no independence needed)
-
Problem 2: no. of heads
- w/ biased coin with head on chance
- what is expectation of heads after flipping it times?
-
- then
- 👨🏫: correct, but ugly!
- simply: use indicator r.v.
- 👨🏫 lesson: life is easier w/ linearity of expectation
-
Problem 3: fair coin toss
- a game w/ fair coin
- keep flipping until you get
- no. of flips
- 👨🏫: what is ?
- intuitively: 2
- proof: let
-
Problem 4: biased coin toss until...
- w/ chance of success:
-
Problem 5: hat-trade
- people in party, with a hat
- each person : leaves w/ hat
- what is: expected no. fo people w/ their own hat?
-
- 👨🏫 hard to compute!
- let : sum of i.r.v.
-
- 👨🏫 so simple!
-
Problem 6 (IMO 1987)
- let be no. of permutations of w/ exactly fixed points
- prove
- divide both sides by , and it's a probabilities problem!
- , where : no. of fixed points
- shown from problem 1
- let be no. of permutations of w/ exactly fixed points
-
Problem 7: coupon collector
- types of coupons, buying a coupon every day
- type: u.a.r.
- let : no. of days of buying coupons
- what is ?
- finding it from
- you can do so with
- 👨🏫 but painful...
- you can do so with
- let : no. of steps to get from -th to -th new type
- let
- (constant)
- as:
- chance of getting a new type:
- as:
- chance of getting a new type:
-
- takes time!
- types of coupons, buying a coupon every day
-
Problem 8: USA MTS
- mathematical talent sets
- play a game: pot starting at H100 to the pot
- if it's tails: pot becomes 0 and get a strike
- 3 strikes: loss
- before each flip: you can claim the pot
- suppose optimal play, what is expected value of earnings?
-
- initially (no. of chances remaining)
-
- flip the coin: if expected value of earning > money in the pot
COMP 2711H: Lecture 35
Date: 2024-11-20 08:45:21
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Markov Chain
-
Markov chain
- stochastic process: sequence of r.v.
- Markov chain
- let be a finite set
- forms a Markov chain if:
- 👨🎓 i.e. no past memory, except for the latest
- let
- where a directed graph
- let be r.v., current vertex at time
- and
- probability space:
- : set of infinite walks on , starting at
- 👨🏫 not countable!
- : set of infinite walks on , starting at
graph LR
1((1));2((2));
1<-->2;1-->1;2-->2;
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span></span></span></span>: event
- let : a finite walk in
-
- 👨🏫 proving that each infinite walk leads to unique event & probability: could be done
- let s.t.
-
Reachability event
- let
-
- aka eventually
-
- for every , is an event
- : finite / countable
- thus, needed
- what if: a path visits a vertex more than once?
- infinite inclusion-exclusion needed
- 👨🏫 instead, we use recurrence
- probability of reaching when the walk starts at
- case works
- case 0: if has no path to
- 👨🏫 ensures unique solution!
- case 1:
- case 2:
- case 0: if has no path to
- let
graph LR
v((v))
u_1((u_1))
u_2((u_2))
u_ext((...))
u_k((u_k))
v--π(v,u_1)-->u_1
v--π(v,u_2)-->u_2
v--π(v,...)-->u_ext
v--π(v,u_k)-->u_k
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mclose">]</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1.0497em;vertical-align:-0.2997em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position:relative;top:0em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:-0.2997em;"><span style="top:-1.7003em;margin-left:0em;margin-right:0.05em;"><span class="pstrut" style="height:2em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.2997em;"><span></span></span></span></span></span></span></span></span></span>
<!-- - further work -->
- e.g.
graph LR
1((1))
2((2))
3((3,T))
4((4))
3--1-->1
1--0.2-->1
1--0.2-->3
1--0.6-->2
2--0.5-->1
2--0.5-->3
4--1-->4
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.7944em;vertical-align:-0.15em;"></span><span class="mord">0.2</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.7944em;vertical-align:-0.15em;"></span><span class="mord">0.2</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.7944em;vertical-align:-0.15em;"></span><span class="mord">0.6</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.7944em;vertical-align:-0.15em;"></span><span class="mord">0.5</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">1</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.7944em;vertical-align:-0.15em;"></span><span class="mord">0.5</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">3</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.5806em;vertical-align:-0.15em;"></span><span class="mord"><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3011em;"><span style="top:-2.55em;margin-left:-0.0037em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">4</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.3669em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">0</span></span></span></span>, according to rule 0
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord">∀</span><span class="mord mathnormal">i</span><span class="mpunct">,</span><span class="mspace"> </span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">0</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.7719em;vertical-align:-0.136em;"></span><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span>
- 👨🏫 for strongly connected component: all <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.0037em;">α</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span> can be a solution
- if there is no edge out of strongly connected
- a BSCC: an SCC without an outgoing edge (bottom)
- claim: in such case, we will reach w/
- for SCC of
- : set of inf. walks seeing infinitely often
- infinite walks that always remain in
- i.e. set of vertex not in
- for the following graph
graph LR
u((u)); v((v))
u--π(u,v)-->v
<!-- further work -->
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mopen">(</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:-0.0576em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.03588em;">v</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord">∣</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:-0.0576em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">u</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mclose">)</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6444em;"></span><span class="mord">1</span></span></span></span> as
- probability of not seeing <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span></span></span></span> after <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">n</span></span></span></span> visits to <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">u</span></span></span></span>
- <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.3669em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">π</span><span class="mopen">(</span><span class="mord mathnormal">u</span><span class="mpunct">,</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mclose">)</span><span class="mclose"><span class="mclose">)</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height:0.6644em;"><span style="top:-3.063em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">n</span></span></span></span></span></span></span></span></span></span></span>
- if <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6986em;vertical-align:-0.0391em;"></span><span class="mord mathnormal">i</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span></span></span></span>: reaching <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span></span></span></span> anyway
- if <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6595em;"></span><span class="mord mathnormal">i</span></span></span></span> is a border vertex:
- it will leave w/ probability 1, as shown above
- if <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6595em;"></span><span class="mord mathnormal">i</span></span></span></span> is not a border vertex:
- it will encounter vertices later in the walk inf. many times
- and so does the border vertex
- thus: it will leave w/ probability 1
- 👨🏫 what if: ?
- 👨🎓 eliminate , until s.t. becomes BSCC..?
- or the other way around, let have multiple predecessors & successors
graph LR
v_1((v_1))
v_2((v_2))
v_3((v_3))
v_t((v_t))
u((u))
vp_1((v'_1))
vp_2((v'_2))
vp_3((v'_3))
vp_t((v'_t))
v_1-->u
v_2-->u
v_3-->u
v_t-->u
u-->vp_1
u-->vp_2
u-->vp_3
u-->vp_t
- however, we can eliminate <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal">u</span></span></span></span>!
- and do so until only <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span></span></span></span> remains
- 👨🏫 thus: it's unique
- 👨🏫 derived problem: what is the probability of reaching the target set infinitely many times?
- see it again and again
COMP 2711H: Lecture 36
Date: 2024-11-25 08:43:58
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Nim: Revisited
-
Nim: with 2 heaps
- Nim: the game with decreasing numbers
- property:
- turn-based
- finite
- impartial
- standard winning condition
- if you can't make a move: you lose
- 2 players
- convert: game into a graph
-
Conversion
- each vertex: state
- if a state can reach , state exist
- the graph: a DAG
- 👨🏫 as the number of states are finite, it
- a state : winning () if, starting from , player 1 wins
- a state : losing () if, starting from , player 1 wins
-
- 👨🏫 there is no way that no one wins!
- each vertex: state
graph LR 0((W)) 1((W)) 2((L)) 3((L)) 4((W)) 5((W)) 6((L)) 0-->1; 0-->3; 1-->2; 1-->5; 3-->1; 3-->5; 4-->0; 4-->3; 4-->5; 5-->2; 5-->6;
- rules
- rule 0: if : no outgoing edges
- then
- rule 1: if s.t. and , then
- optimal players!
- rule 2: if s.t. , then
- rule 0: if : no outgoing edges
- and: apply rules only if all its successors are covered
- aka topological ordering: given a DAG , topological order:
- permutation of vertices s.t. then appears before
- 👨🏫 in our case, we want the reverse: thus, just inverse the order
- theorem: every DAG has a topological order
-
Nim with heaps
- with natural numbers:
- each player: choosing a no. and decrease it in their turn
- theorem: state of winning: depends on of all
-
- intuition: you lose when too
-
- suppose:
- then player: changes to
- e.g. initially:
- then
- similarly, means:
- yet: showing existence of move leading to win is hard
- for , there exists index s.t.
- deduction resulting from XOR: always possible
- 👨🏫 for the first encounter of in result, pick a number that is in that digit
- with natural numbers:
-
Nim with 1 heap
- e.g. when , its graph :
graph LR
5((5))
4((4))
3((3))
2((2))
1((1))
0((0))
5-->4; 4-->3; 3-->2; 2-->1; 1-->0
2-->0;
3-->1; 3-->0;
4-->2; 4-->1; 4-->0;
5-->3; 5-->2; 5-->1; 5-->0;
- and for heap: it's Cartesian product of each
- Sprague–Grundy theorem
-
Sprague-Grundy theorem
- every game: winning conditions can be found, like Nim
- actually: you can convert any game into Nim!
- assign a nimber to every vertex in each :
- rule 0: if has no outgoing edge:
- rule 1: otherwise:
- there might be a case: where path exist and
- 👨🏫 however, it doesn't really matter: the other player can undo the move!
- thus, we can ignore this move!
- 👨🏫 however, it doesn't really matter: the other player can undo the move!
- and there is a corner case: where neighbors have the same nimber
- which doesn't exist
-
Reverse Nim
- w/ two natural numbers and two players
- in each turn, a player can:
- decrease
- decrease
- decrease both to
- goal: not giving two equal numbers to opponents
- 👨🏫 exercise: find for this game
COMP 2711H: Lecture 37
Date: 2024-11-25 17:59:16
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
One-Shot Game
-
One-shot game
-
players: making a move making a move all at once
-
example: prisoner's dilemma
- as prisoners cannot communicate, their action: pseudo simultaneous
- if both remains silent: 2 yr to each
- if both confess: 4 yr to each
- if only one confess: 1 yr to confessor, 5 yr to another
-
👨🏫 consider it as a matrix
Confess Silent Confess Silent -
assume rational behavior of prisoners:
- working for his / her own interest
- not about their old colleague anymore
- maximizing their benefit, or minimizing their cost in this case
- working for his / her own interest
-
for total sum: is ideal
-
however: do case analysis
- if confess: better confess too, it minimizes the year
- if remains silent: better confess, again
- it minimizes the year
- thus: is better confess
- ... as the table is symmetric: both gets to confess
- and gets year each
-
-
Generalization
- a one-shot game w/ players consists of:
- a set for strategies for player
- a payoff function
- assumption: players maximize their own profit
- 👨🏫 definition of "rational"!
- each player : chooses a strategy
- the outcome:
- define
- : replace to , preserving the rest
- a one-shot game w/ players consists of:
-
Dominant strategy
- strategy : dominant if
- no matter what other people do: doing is always the best
- but game with dominant strategy: often badly designed
- strategy : dominant if
-
Example: pollution game
- modelling global CO2 emission stuff
- choice: pollute / not
- stop polluting: costs 5
- polluting: every country loses 1
- e.g. for pollutants: every country loses
- additional 5 for countries who stopped polluting
- e.g. for pollutants: every country loses
- dominant strategy: to pollute, for everyone
- thus: every country will have cost of
- while we could have cost of each otherwise
- 👨🏫 don't pollute :p
- 👨🎓 so should we be irrational..?
-
Counter example: Battle of sexes
-
boy & girl: want to spend evening together
- boy: wants to watch baseball
- girl: wants to watch softball
-
"payoff" matrix
Baseball Softball Baseball Softball -
no dominant strategy exists
- we must find: equilibrium
- e.g. if we are in baseball, baseball:
- no one would want to change: as neighbors provide less benefit
- same for softball, softball
- 👨🏫 aka Nash equilibrium
-
-
Nash equilibrium
- outcome : a Nash equilibrium if:
- i.e. no one has motivation to change
- 👨🏫 economics / psychology people say: it makes sense if it's repeated
but psychology is not science
- equilibrium: weaker notion of idea
- 👨🏫 is there a game without nash equilibrium?
- Rock Paper Scissors!
- outcome : a Nash equilibrium if:
-
Example: rock paper scissors
R P S R P S - no "pure" Nash equilibrium
-
Example: matching pennies
-
guessing the opponent's (dishonest) coin flip (=side choice!)
H T H T -
no "pure" Nash equilibrium
-
-
Mixed Nash equilibrium
- a mixed strategy for player :
- : set of strategies for player
- behavior of others: can't be predicted
- thus: redefine rational
- into maximizing "expected profit"
- each player : chooses a mixed strategy
- then outcome: where
- mixed Nash equilibrium:
- a Nash equilibrium if:
- for RPS: uniform random is a mixed Nash equilibrium
- 👨🏫 you can compute the expected value yourself
- 👨🏫⭐⭐ Nash's Nobel prize-worth theorem:
- any -player game in which every is finite has a mixed Nash equilibrium
- 👨🏫 proof: not coverage of 2711H. However, it's around Ch. 20 in the book
- w/ infinite players or infinite strategies: it doesn't hold
- sadly, we don't know how to compute the equilibrium in polynomial time
- 👨🏫 just know that this exist!
- a mixed strategy for player :
COMP 2711H: Lecture 38
Date: 2024-11-27 02:52:39
Reviewed:
Topic / Chapter:
summary
❓Questions
Notes
Lecture
-
Arena
- arena: a directed graph
- s.t.
- 👨🏫: ownership of graph: must also be defined
- 👨🏫 assume it to be finite (in this course), although it's not explicitly mentioned
- game: arena and starting vector
- owner of new vertex: gets to make next decision
- goal: making move within one's own
- others' goal: preventing the player from doing so
- example
- arena: a directed graph
graph LR
0(( ))
1(( ))
2( )
3(v_0)
0-->2; 0-->1; 1-->0; 1-->2; 2-->2; 3-->0; 3-->1
- strategy: strategy for player :
- function
- if
- walk: can be done infinitely as all nodes have at lease one outdegree
- outcome: infinite walk on starting at
- use for the set of all outcomes
- if : strategies for players
- then : corresponding outcome
-
Objective
- objective for player 1: a strategies
- zero-sum game:
- i.e. victory of one: defeat of one
- 👨🏫 non-zero sum game: also interesting
- where loss of a player does not necessarily mean loss of another
- strategy for player 1: winning strategy if:
- for every , we have
- i.e. regardless of other players' action, outcome is in your objective
- 👨🏫: same for non-zero sum game
- losing condition can also be defined
- 👨🏫 but "lose" is not well defined for non-zero sum game...
- game : determined if, for every starting vertex
- either or (or: ) has a winning strategy
- objective for player 1: a strategies
-
Hint for problem set 11
- let there be a game w/ both players having no winning strategy
- e.g. rock scissor paper intuitively
- how can we make this in a graph game?
- think about infinite objective
- let there be a game w/ both players having no winning strategy
-
Reachability game
- player 1's objective: to reach
-
- 👨🏫 game: also can be called as safety game
- a zero-sum game
- 👨🏫 diamond notation: from linear-time temporal logic (LTL)
- input: arena
- target set
- output:
- rules
- if and and
- then
- if and , we have
- then
- algorithm:
- : set of starting vertices player 1 wins in steps
- compute
- algorithm: terminates as there are finite no. of vertices
- cannot increase infinitely
- terminate when
- yet: we must also show that player 2 has strategy if:
- if :
- it has no edge to
- if so: player 1 will go to
- it has no edge to
- if :
- it has at least an edge to stay in
- as: player 2 has no reason to run into defeat
- player 2's strategy: simply
- theorem: ,
- winning strategy for player 1: move into an inner circle ()
- always succeeds: as is expanded that way
- must also ensure: the game is memory-less
- computation of : dependent on arena, not history
- winning strategy for player 1: move into an inner circle ()
- 👨🏫 let's make it more complicated (even in last session)
- player 1's objective: to reach
-
Büchi game
- goal: to visit infinitely many times
- input: arena
- target set
- output:
- 👨🏫 whether it's determinant or not: not shown
- from there: show that
- ,
- known:
-
- known:
- if: the game starts outside :
- player 1 doesn't want to land
- i.e. for all , has at least one edge not going
- 👨🏫 reduce the problem by removing all edge going into / vertices in
- remainder: still a valid game
- 👨🏫 reduce the problem by removing all edge going into / vertices in
- total algorithm
-
-
-
- algorithm: terminates as there are finite vertices
-
- what if: stuck? i.e.
- then, let
-
- : empty
- within : one can reach arbitrarily (infinitely) many times
- theorem: ,
- player 2: simply staying within the smallest inner circle possible
- = memory-less
- player 1: don't step outside of smaller game
- don't join
- = memory-less
- if it's already in : just pick any
- as player 1 will lose anyway
- don't join
- player 2: simply staying within the smallest inner circle possible
- what if: we have combinations of the objectives?
- e.g. player 1 want to reach both ?
- once, or infinitely many times?
- 👨🏫 def. on your final, and it's non-trivial
- 👨🏫 solution available in Wikipedia, but involves extra concepts outside syllabus
- e.g. player 1 want to reach both ?
COMP 2711H Reading
- Lecture 1: Propositional Logic
- Lecture Video
- Reading: Chapter 2 of Grimaldi (Fundamentals of Logic)
- Video: Proofs
- Lecture 2: Predicate Logic and Peano's Axioms
- Lecture Video
- Reading: Chapter 2 of Grimaldi (Fundamentals of Logic)
- Video: Peano Axioms
- Lecture 3: Induction, Well-ordering and Infinite Descent
- Lecture 4: Induction Problems and Strong Induction
- Lecture Video
- Video: Strong Induction
- Video: Proof by Strong Induction
- Video: Strong Induction Examples
- Reading: Chapters 3 and 8 of Engel (The Extremal Principle, The Induction Principle)
- Lecture 5: Solving More Induction Problems
- Lecture Video
- Video: Induction Problems
- Video: Divisibility Problems Solved by Induction
- Video: Epic Induction
- Reading: Chapters 3 and 8 of Engel (The Extremal Principle, The Induction Principle)
- Lecture 6: Counting, Permutations, Combinations, Balls and Walls
- Lecture Video
- Reading: Chapter 1 of Grimaldi (Fundamental Principles of Counting)
- Reading: Chapter 1 of Chen and Koh (Permutations and Combinations) -- Very Important
- Reading: Chapter 1 of Ross (Combinatorial Analysis)
- Fun to Read: Which Rectangular Chessboards Have a Knight's Tour?
- Lecture 7: Solving Counting Problems
- Lecture Video
- Reading: Chapter 1 of Chen and Koh (Permutations and Combinations) -- Very Important
- Lecture 8: More Counting
- TA Session 1
- Lecture 9: Principle of Inclusion and Exclusion
- Lecture Video
- Reading: Chapter 2 and 4 of Chen and Koh (Binomial Coefficients, Inclusion-Exclusion)
- Video: Inclusion-Exclusion Example
- Video: 3-set PIE
- Video: Counting using PIE
- Lecture 10: Generalized Principle of Inclusion and Exclusion (23 September 2023)
- Lecture Video
- Reading: Chapter 2 and 4 of Chen and Koh (Binomial Coefficients, Inclusion-Exclusion)
- Reading: Chapter 8 of Grimaldi (Inclusion-Exclusion)
- Video: Inclusion-Exclusion
- Video: PIE Problems
- Video: Generalized PIE
- Video: Derangements
- Lecture 11: Pigeonhole Principle
- Lecture Video
- Reading: Chapter 3 of Chen and Koh (Pigeonhole and Ramsey)
- Reading: Chapter 4 of Engel (Box Principle)
- Video: Pigeonhole Principle
- Video: Pigeonhole Principle Examples
- Video: Pigeonhole Principle - Establishing a Pattern
- Video: Pigeonhole Principle - Generalizing the Cases
- Playlist: More Advanced Pigeonhole Principle Problems
- TA Session 2
- Lecture 12: Graphs, Trees, Paths and Walks
- Lecture Video
- Reading: Sections 1.1 and 1.2 of West (What is a Graph?, Paths, Cycles and Trails)
- Video Playlist: Introduction to Graph Theory
- Video Playlist: Watch Lectures 1 to 4
- Lecture 13: More Theorems on Graphs and Trees
- Lecture Video
- Reading: Sections 1.3 and 1.4 of West (Vertex Degrees & Counting, Directed Graphs)
- Video Playlist: Watch from 10.1.1 to 11.1.1
- Recommended to Watch: Graph Theory Background
- Lecture 14: Even More Theorems on Graphs and Trees
- Lecture Video
- Reading: Sections 2.1 and 2.2 of West (Trees and Distance: Basic Properties, Spanning Trees)
- Recommended to Watch: DFS and BFS
- Reading: Chapters 11 and 12 of Grimaldi (Graph Theory, Trees)
- TA Session 3
- Lecture 15: Minimum Spanning Trees, Directed Graphs, DAGs
- Lecture Video
- Video: Kruskal's Algorithm
- Video: Prim's Algorithm
- Video: Minimum Spanning Trees
- Reading: Chapters 1 and 2 of West (Fundamental Concepts, Trees and Distance)
- Lecture 16: Tree-based Algorithms and Huffman Coding
- Lecture Video
- Reading: Section 2.3 of West (Optimization and Trees)
- Video: Huffman Coding and Huffman Trees
- Video: Huffman Coding Example
- Recommended Video: Huffman Coding + Code
- Recommended Video: Dynamic Programming on Trees
- Lecture 17: Distance, Shortest Paths and Matchings
- TA Session 4
- Lecture 18: Matchings, Vertex Covers, Edge Covers and Independent Sets
- Lecture Video
- Reading: Section 3.1 of West (Matchings and Covers)
- Lecture 19: Network Flow and the Ford-Fulkerson Algorithm
- Lecture Video
- Reading: Section 4.3 of West (Network Flow Problems)
- Video: Maximum Flow and Ford-Fulkerson
- Video: Flow Networks and Maximum Flow
- Video: Maximum-Flow Minimum-Cut Algorithm
- Video: Max-flow and Ford-Fulkerson
- Video: Ford-Fulkerson in 5 minutes
- Lecture 20: Stable Matchings and Graph Coloring
- Lecture Video
- Reading: Subsection 3.2.3 of West (Stable Matchings)
- Reading: Section 5.1 of West (Vertex Colorings and Upper Bounds) -- Brooks' Theorem is not part of the syllabus
- Video: Introduction to Graph Colouring
- Video: Coloring Code - How Compilers Use Graph Theory
- Video: Applications of Graph Colouring
- Midterm Exam
- Lecture 21: Divisibility and Greatest Common Divisor
- Lecture Video
- Reading: Chapters 1 and 2 of Burton (Preliminaries, Divisibility Theory)
- Video: Number Theory I
- Playlist: Introduction to Number Theory (Watch Lectures 3 and 4)
- Lecture 22: Prime Factorizations and the Fundamental Theorem of Arithmetic
- Lecture Video
- Reading: Sections 2.4 to 3.3 of Burton (Euclid to Goldbach)
- Video: Primes
- Solve Problems 1 to 10 of ProjectEuler.net
- Fun to read: Collatz Conjecture
- Lecture 23: Congruence, Modular Multiplicative Inverse and the Chinese Remainder Theorem
- Lecture Video
- Reading: Chapter 4 of Burton (Congruences)
- Video Playlist: Chinese Remainder Theorem
- Solve Problems 14, 20, 27, 47, 50, 69, 77, 112, 122 and 451 of ProjectEuler.net
- TA Session 5
- Lecture 24: Fermat's Little Theorem, Euler's Theorem, Wilson's theorem
- Lecture Video
- Video: Order of an integer modulo n
- Video: Fermat's Little Theorem
- Video: Euler's Theorem
- Video: Wilson's Theorem
- Playlist: Introduction to Number Theory (Watch Lectures 5 to 14, Primes to Euler's Totient)
- Video: COMP 4541's Number Theory Tutorial - Part II
- Video: Proof that the Totient Function is Multiplicative
- Video: Explicit Formula for Euler's Totient Function
- Video: Euler's Totient Theorem and Fermat's Little Theorem
- Reading: Chapters 5 and 7 of Burton (Fermat's Theorem, Euler's Generalization of Fermat's Theorem)
- Lecture 25: Diffie-Hellman-Merkle Key Exchange and ElGamal Encryption
- Lecture Video
- Video: Secret Key Exchange
- Video: The Mathematics behind Diffie-Hellman
- Video: COMP 4541's Diffie-Hellman Lecture
- Video: COMP 4541's Number Theory Tutorial - Part I
- Video: COMP 4541's ElGamal Lecture
- Video: ElGamal Encryption
- Reading: Recommended Chapter 10 of Burton (Intro to Crypto)
- Lecture 26: RSA Encryption and Digital Signatures
- Lecture Video
- Video: Breaking RSA
- Video: What are Digital Signatures?
- Video: COMP 4541's RSA Lecture
- Video: COMP 4541's Digital Signatures Lecture
- Video: The RSA Cryptosystem and Efficient Exponentiation
- Video: Diffie-Hellman Key Exchange and the Discrete Log Problem
- Reading: Side-channel Attacks (Wikipedia)
- Reading: Power Analysis (Wikipedia)
- TA Session 6
- Lecture 27: Russell's Paradox and Zermelo–Fraenkel Axioms
- Lecture 28: Axiom of Infinity and Bijections
- Lecture 29: Countability and the Theorems of Cantor, Tarski and Schröder–Bernstein
- TA Session 7
- Lecture 30: The Set of Real Numbers
- Lecture 31: |ℝ|=|P(ℕ)| and the Axiom of Choice
- Lecture 32: Introduction to Probability Theory
- Lecture Video
- Reading: Chapter 2 of Ross (Axioms of Probability), including sections marked by *
- TA Session 8
- Lecture 33: Conditional Probability, Independence and Expectation
- Lecture Video
- Read: The Monty Hall Problem
- Read: The Sleeping Beauty Problem
- Watch: Philosophers are not smart enough for probability theory!
- Reading: Chapters 3 and 4 of Ross (Conditional Probability, Independence, Random Variables)
- Video: Bayes Theorem
- Video: The Bayesian Trap
- Lecture 34: Solving Problems using Linearity of Expectation
- Lecture 35: Markov Chains
- Lecture 36: Nim and the Sprague-Grundy Theorem
- Lecture 37: One-shot Games and Nash Equilibria
- Lecture Video
- Video: Nash Equilibrium in 5 Minutes
- Video: Prisoners' Dilemma
- Video: Repeated Prisoners' Dilemma
- Reading: Chapter 1 of the Algorithmic Game Theory Book (Basic Solution Concepts)
- Lecture 38: Two-player Infinite-duration Games on Graphs
- TA Session 9
- TA Session 10
- TA Session 11