COMP 2711H: Lecture 8

Date: 2024-09-16 17:59:47

Reviewed: 2024-10-07 02:49:12

Topic / Chapter:

summary

❓Questions

Notes

Revisiting Problem

Problem 2
- how many ways can we put $n$ distinct people around $r$ identical circles, while ensuring 1 and 2 are next to each other
- simply: glue 2 people together
- thus $s (n - 1, r)$ , and times 2 as you can order between two people can swapped
  - however: if there is a circle w/ two people only:
    - ordering doesn't matter
  - i.e. $s (n - 2, r - 1)$ cases are counted twice
- finally: $2 \cdot s (n - 1, r) - s (n - 2, r - 1)$
- then subtract it from the real, total, number to find how many ways aan we allocate people while separating the two
- $∴ s (n, r) - 2 \cdot s (n - 1, r) + s (n - 2, r - 1)$
Weekly Problem 5
- $73!$ ways of ordering boys
- are there are 74 slots we can insert girls
  - and at most 1 girls can be inserted / slot
  - i.e. $(9 74)$
  - however, as order of girls matter too, so
- $∴ a [b, g] = 73! 9! (9 74)$
- 👨‍🏫 this leads to new method of solving the equation!
  - if $x_{1} + x_{2} + x_{3} + x_{4} = 7; x_{i} \geq 1$
  - i.e. if we have constraint: $x_{1} \geq 1$
  - then we only have only 6 slots (7-1) to insert 3 bars (4-1)
- part 4: we cannot have 3 consecutive girls
  - 👨‍🏫 casework: better done on girls, as we have much less girls than boys
  - girls: divided into conseq. groups of 1/2 (not 3)
  - 👨‍🎓 ~= counting problem? how many ways to pay 9 dollar w/ 1 dollar and 2 dollar banknotes? orders matter
    - 👨‍🏫 $9 = 1 + 2 + 1 = 2 + 1 + 2$
  - $α [n, t] :=$ no. of ways to write $n$ as sum of $t$ summands of 1 or 2
    - 👨‍🎓 summand: operand of summation
    - if last summand is $1$ : $α [n - 1, t - 1]$
    - if last summand is $2$ : $α [n - 2, t - 1]$
    - $α [1, 1] = 1; α [2, 1] = 1; α [0, t] = 0; α [n, 0] = 0$
  - thus $α [n, t] = α [n - 1, t - 1] + α [n - 2, t - 1]$
    - thus: total of ways on grouping & ordering girls are as of following $i = 5 \sum 9 α [9, i] \cdot 9!$
    - $5$ for min. groups of girls; $9$ for max.
  - back to boys, we have $i + 1$ slots to put boys
    - $b_{0} + b_{1} + \dots + b_{i} = 73$
    - $b_{0}, b_{i} \geq 0$
    - $b_{1}, b_{2}, \dots, b_{i - 1} \geq 1$
    - and let's denote the no. solution as $β_{i}$
      - 👨‍🎓 $i$ bars w/ $73 - (i - 1) = 74 - i$ balls
      - $(i 74)$
  - for real, finally:
    - $\sum_{i = 5}^{9} α [9, i] \cdot 9! \cdot β_{i} \cdot 73!$
    - as all boys are distinct as well
    - computable by hand (unlike previous recursion)
  - computing $α$ better:
    - $a [n, t] = \frac{t !}{( n - t )! ( n - 2 \cdot ( n - t ))!} = \frac{t !}{( n - t )! ( 2 t - n )!}$
    - $t$ coins, with $n - t$ 2-coins and $n - 2 \cdot (n - t) = 2 t - n$ 1-coins
Weekly problem 7
- 10 R's and 6 U's, can be presented as
- $x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} + x_{7} = 10$
  - $x \geq 0$
  - aka $(6 16)$
- or, the other way:
  - $y_{1} + y_{2} + \dots + y_{11} = 6$
  - $y \geq 0$
  - aka $(10 16) = (6 16)$
Weekly problem 8
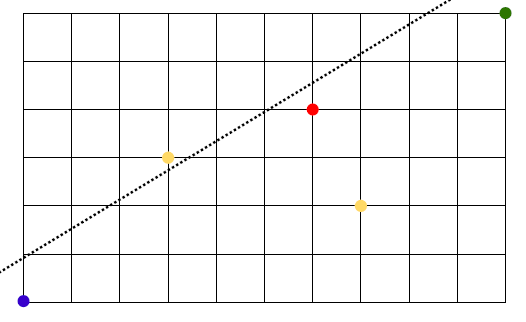
- how many no. of ways from blue to red does NOT go through red point?
  - total ways: $(6 16)$
  - total ways B->R: $(4 10)$
  - total ways R->G: $(2 6)$
  - finally: $(6 16) - (4 10) (2 6)$
Weekly problem 9
- how many no. of ways from blue to red does NOT go through yellow point?
- however: no path can go through both yellow points!
Weekly problem 10
- how many paths do we have that do not cross the dotted line?
- like Pascal's triangle, or Fibonacci numbers, you can simply add up paths from two points together!
Problem 8 from 102 problems
- Spider with 8 legs
- w/ 8 socks ( $s_{i}$ ) and 8 shoes ( $r_{i}$ )
- and how many permutations are there, that spider wears $s_{i}$ before corresponding $r_{i}$ ?
- first, there are $16!$ ways
  - however, there is a double counting per each leg, correct order & incorrect order
  - thus, $\frac{16 !}{2 ^{8}}$
- instead, it's like a sequence of size 16 s.t. each number 1-8 appears exactly twice
  - count the first one as socks, second as shoes
  - finally, 16 numbers with 8 groups of 2 indistinct numbers
    - so $\frac{16 !}{( 2 ! ) ^{8}} = \frac{16 !}{2 ^{8}}$
Divisors
- how many divisors does 640 have?
- $640 = 2^{7} \cdot 5$
- 16 divisors! as all its divisor will look like $2^{x} 5^{y}$
  - where $x \in [0, 7], y \in [0, 1]$
- how many common divisors do 100 and 640 have?
  - $100 = 2^{2} \cdot 5^{2}$
  - and all common divisor: in $2^{x} 5^{y}$
  - s.t $x \in [0, 2], y \in [0, 1]$
  - i.e. min appearing size of either
  - $∴ 3 \cdot 2 = 6$ ways
  - 👨‍🏫 also, $g cd (640, 100) = 2^{2} \times 5^{1}$
    - and all divisor of $g cd$ : common divisor of both numbers

COMP 2711H: Honors Discrete Mathematical Tools for Computer Science