COMP 2711H: Lecture 7

Date: 2024-09-16 02:53:37

Reviewed: 2024-10-07 02:47:38

Topic / Chapter: More Counting Problems

summary

❓Questions

Notes

Arrangement Along the Circle

Problem 1
- how many ways can $n$ people sit around a circle?
- rotation / shifting of an arrangement: is considered equivalent / same permutation
- $\frac{n !}{n} = (n - 1)!$
Problem 2
- how many ways cab we put $n$ distinct people around $r$ identical circles?
  - i.e. no. of tables
- assume: $r ∣ n$ ?
- find relation using induction-like approach
- 👨‍🏫 let's notate the solution as $s (n, r)$
- base case: $s (n, 1) = (n - 1)!$
- person $n$ is either
  1. in a circle on their own: $s (n - 1, r - 1)$
    - as we need to place the rest
  2. sharing a circle
    - how many ways can we insert?
    - at least $r$ ways, as there are $r$ tables
    - $(n - 1) \cdot s (n - 1, r)$
    - as there are $n - 1$ people already on the table, and we are choosing, "who is on the left?"
- $s (n, r) = s (n - 1, r - 1) + (n - 1) \cdot s (n - 1, r)$
Problem 3
- in how many ways can we $n$ people around circle if 2 people must not be next to each other?
- $(n - 2)! \cdot (n - 3)$
- as there are $(n - 2)!$ ways of ordering $n - 1$ people around the table.
- 👨‍🏫 or:
  - no. of ways to put them together(when $n \neq = 2$ ), $(n - 2)! \cdot 2$
  - and there are $(n - 1)!$ total permutation
  - thus $(n - 2)! ((n - 1) - 2)$
Problem 4
- how many ways cab we put $n$ distinct people around $r$ identical circles?
  - if 2 people must not be next to each other?
- case: no. of ways to put two people together
  - case 1: setting up a new table for them
    - $s (n - 2, r - 1)$
  - case 2: sharing table w/ $i$ people
    - $2 \cdot (i n - 2) i! s (n - 2 - i, r - 1)$
- finally: $s (n, r) = s (n - 2, r - 1) + \sum_{i = 1}^{n - 2} 2 \cdot (i n - 2) i! s (n - 2 - i, r - 1)$
  - (and subtracted from all no. of permutations)
  - ❓ can't we simply treat two people as one?
  - i.e. $s (n, r) = s (n - 1, r) /2$
Problem 5
- let $A$ be a set of $2 n$ elements
  - what is the no. of pairings in $A$
  - 👨‍🏫 $iπj ⟺ jπi$
  - and no element can be pair of itself
- solution 1
  - steps
    - after choosing an element, there are $2 n - 1$ ways to choose its pair
    - after choosing the next element, there are $2 n - 3$ ways to choose its pair
    - ...
    - after choosing the penultimate element, there are 1 way to choose its pair
  - i.e. $\prod_{i = 1}^{n} (2 n - 2 i + 1)$
- solution 2
  - simply showing all linear permutations
  - and grouping them together $(a_{1}, b_{1}), (a_{2}, b_{2}), \dots$
  - there are $(2 n)!$ ways to ordering the elements
  - and $n!$ ways to order different groups and $2^{n}$ ways to order $n$ groups within it
  - thus $\frac{( 2 n !)}{n ! 2 ^{n}}$
- solution 3
  - if order is accounted:
    - $(2 2 n) (2 2 n - 2) (2 2 n - 4) \dots (2 2)$
  - and there are $n!$ different ways to order them
  - thus, $\frac{\prod _{i = 1}^{n} ( 2 2 i )}{n !}$

Weekly Problems

Problem 1: Week 2
- how many permutations $π$ of $n$ people satisfy $\forall i, π [i] \neq = i$ ?
- 👨‍🏫 aka: derangement
- show recursive solution
- let $d_{n} :=$ no. of ways to arrange w/ $n$ people / elements
- $d_{0} = 1$ (similar logic as $F ⟹ q$ then $q$ )
- $d_{1} = 0$
- $d_{2} = 1$
- general cases
  - person $n$ sits on chair $1 \leq i < n$
  - two cases
    1. $i$ sits on chair $n$ ( $d_{n - 2}$ )
    2. $i$ does not sit on chair $n$
      - $d_{n - 1}$
      - as: each people (except $n$ ): has exactly ine forbidden sit
        
        for $j \neq = i$ : $j$
        
        for $i$ : $n$ (as that is the condition)
      - so: it's a direct subproblem of size $n - 1$
  - solution: $d_{n} = (n - 1) \cdot [d_{n - 2} + d_{n - 1}]$
    - i.e. no. of choosing $i$ , then recurrence holds for each cases
Problem 5: Week 2
- 73 boys, 9 girls; 82 total
- how many permutations s.t. all girls appear before all boys?
  - $9! 73!$
- part 2: having 7 girls in top half, and 2 girls in bottom half
  - top half: 7 girls & 34 boys
  - bottom half: 2 girls & 39 boys
- one of the solution:
  - choose who will go in the top half
    - $(7 9) (24 73)$
    - (no need to choose who will go in the bottom, as those are complements from top half)
- part 3: no two girls are next to each other
  - detour:
    - no. of solutions of $x_{1} + x_{2} + x_{3} = 10$ ; $x \geq 0$
    - consider: 10 blocks, separated by 2 (=3-1) bars
      - there are 11 slots total
      - so $(2 11)$
    - no. of solutions of $x_{1} + x_{2} + x_{3} = 10$ ; $x \geq 1$
      - let $y_{i} = x_{i} - 1$
      - then the same condition!
      - thus: $\sum y_{i} = b - n$
  - similarly: consider girls as blocks, and boys as bars
  - first, there are $9!$ ways to order the girls
    - and let $b_{0}, \dots b_{9}$ no. of boys after girl $i$ (and $b_{0}$ : no. of boys before girl 1)
  - $\sum b_{i} = 73$
  - $b_{1}, \dots d_{8} \geq 0$ ; $b_{1}, b_{9} \geq 0$
  - let:
    - $c_{0} = b_{0}; c_{9} = 0$
    - and for all others: $c_{i} = b_{i} - 1$
    - now we have $\sum c_{i} = 73 - 8 = 65$
    - thus: $(65 + 9)!$
  - however, boys (nor girls) are considered distinct
    - so: $\frac{74 !}{65 ! 9 !}$
- and with permutations:
  - $9! 73! \frac{74 !}{65 ! 9 !}$
- part 4: no three girls are next to each other
  - one solution: adding constraints, such as: $b_{i} + b_{i + 1} \geq 1$
  - let $a [b, g]$ : no. of solutions for the question
  - solution: either starts w/ boy or a girl
    - case 1: seq. starts w/ a boy
      - as any boy can be the first
      - $b \cdot a [b - 1, g]$
    - case 2: seq. starts w/ exactly one girl?
      - $g$ ways to choose
      - $g \cdot b \cdot a [b - 1, g - 1]$
    - case 3: seq. starts w/ exactly two girls?
      - $g \cdot (g - 1) \cdot b \cdot a [b - 1, g - 2]$
  - $a [b, g] = b \cdot a [b - 1, g] + g \cdot b \cdot a [b - 1, g - 1] + g \cdot (g - 1) \cdot b \cdot a [b - 1, g - 2]$
  - 👨‍🎓 how about the base case..?
Problem 6
- how many rectangles are there?
- i.e. $0 \leq x_{1} \leq x_{2} \leq 10$
  - and $0 \leq y_{1} \leq y_{2} \leq 6$
- finally: $(2 11) (2 7)$
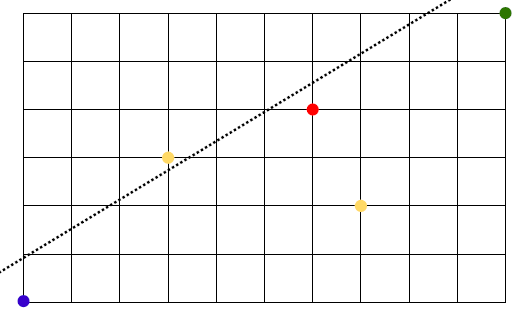
Problem 7
- how many ways are there of moving, from blue to green?
- 👨‍🏫 you can only move up & right
- so there are 16 possible moves, 10 being R and 6 being U
- thus: $\frac{16 !}{10 ! 6 !}$

COMP 2711H: Honors Discrete Mathematical Tools for Computer Science